题目内容
等差数列{an}中,a7=4,a19=2a9(2)设bn=
,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,Sn是数列{bn}的前n项和,求使sn>8-n成立的n的最小值.
| 1 |
| 2nan |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| 2nan |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,根据题意和等差数列的通项公式列出关于首项、公差的方程,代入通项公式化简;
(2)由(1)和题意求出bn,利用裂项相消法求出Sn,代入sn>8-n求出n的范围,再由n取整数求出n的最小值.
(2)由(1)和题意求出bn,利用裂项相消法求出Sn,代入sn>8-n求出n的范围,再由n取整数求出n的最小值.
解答:
解:(1)设等差数列{an}的公差为d,
则由an=a1+(n-1)d得:
,
解得a1=1,d=
,
所以{an}的通项公式为an=
-----------(4分)
(2)因为bn=
=
=
-
,-----------(6分)
所以Sn=(
-
)+(
-
)+…+(
-
)=
---------------(8分)
由sn>8-n得1-
>8-n,解得n>3+
或n<3-
又n∈N*,所以满足条件的n的最小值为8--------------------(10分)
则由an=a1+(n-1)d得:
|
解得a1=1,d=
| 1 |
| 2 |
所以{an}的通项公式为an=
| n+1 |
| 2 |
(2)因为bn=
| 1 |
| 2nan |
| 2 |
| 2n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以Sn=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
由sn>8-n得1-
| 1 |
| n+1 |
| ||
| 2 |
| ||
| 2 |
又n∈N*,所以满足条件的n的最小值为8--------------------(10分)
点评:本题考查了等差数列的通项公式,以及数列的求和方法:裂项相消法,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知函数f(x)的定义域为[1,3],则函数f(2x-1)的定义域为( )
| A、[1,2] |
| B、[1,5] |
| C、[2,4] |
| D、[1,4] |
已知a=(
)
,b=(
)
,c=
则( )
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<c<a |
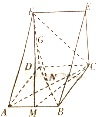 已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.
已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.