题目内容
下列命题中正确命题的个数是( )
(1)对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1>0;
(2)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
(3)已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
=1.23x+0.08
(4)若函数f(x)是定义在R上的奇函数,且f(x+4)=f(x),则f(2012)=0.
(1)对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1>0;
(2)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
(3)已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
| ? |
| y |
(4)若函数f(x)是定义在R上的奇函数,且f(x+4)=f(x),则f(2012)=0.
| A、2 | B、3 | C、4 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1)中,由命题p写出它的否定¬p,判定命题(1)是否正确;
(2)中,求出直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m的取值,即可判定命题(2)是否正确;
(3)中,由回归直线过样本中心点,求出回归直线方程,即可判定命题(3)是否正确;
(4)中,通过函数的关系式,求出函数的周期,利用奇函数直接判断结果即可.
(2)中,求出直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m的取值,即可判定命题(2)是否正确;
(3)中,由回归直线过样本中心点,求出回归直线方程,即可判定命题(3)是否正确;
(4)中,通过函数的关系式,求出函数的周期,利用奇函数直接判断结果即可.
解答:
解:对于(1),命题p:?x∈R,使得x2+x+1<0的否定是¬p:?x∈R,均有x2+x+1≥0;∴命题(1)错误.
对于(2),∵直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m(m+3)-6m=0,即m=0或m=3,
∴m=3不是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;∴命题(2)错误.
对于(3),∵回归直线为
=bx+a的斜率的值为1.23,直线过样本点的中心(4,5),
∴a=0.08,∴回归直线方程是为
=1.23x+0.08;∴命题(3)正确.
对于(4),函数f(x)是定义在R上的奇函数,且f(x+4)=f(x),∴f(0)=0,并且函数的周期是4,
∴f(2012)=f(503×4)=f(0)=0,∴(4)正确.
故选:A.
对于(2),∵直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直时,m(m+3)-6m=0,即m=0或m=3,
∴m=3不是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;∴命题(2)错误.
对于(3),∵回归直线为
| ? |
| y |
∴a=0.08,∴回归直线方程是为
| ? |
| y |
对于(4),函数f(x)是定义在R上的奇函数,且f(x+4)=f(x),∴f(0)=0,并且函数的周期是4,
∴f(2012)=f(503×4)=f(0)=0,∴(4)正确.
故选:A.
点评:本题通过命题真假的判定,考查了命题的否定、充分与必要条件、回归直线方程的知识,解题时应对每一个命题认真分析,以便作出正确的选择,是综合性题目.

练习册系列答案
相关题目
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
常说“便宜没好货”,这句话的意思是:“不便宜”是“好货”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知x,y之间的数据如下表所示,则y与x之间的线性回归方程必过点( )
| x | 1.08 | 1.12 | 1.19 | 1.30 |
| y | 2.25 | 2.37 | 2.40 | 2.60 |
| A、(0,0) |
| B、(1.17,0) |
| C、(0,2.41) |
| D、(1.17,2.41) |
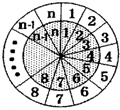 如图所示的两个同心圆盘均被n等分(n∈N+且n≥2),在相重叠的扇形格中依次同时填上1,2,3,L,n,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
如图所示的两个同心圆盘均被n等分(n∈N+且n≥2),在相重叠的扇形格中依次同时填上1,2,3,L,n,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.