题目内容
常说“便宜没好货”，这句话的意思是：“不便宜”是“好货”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据逆否命题的等价性和充分条件必要条件的定义进行判断．
解答：
解：“好货不便宜”是“便宜没好货”的逆否命题，
根据互为逆否命题的真假一致得到：“好货不便宜”是真命题．
所以“好货”⇒“不便宜”，
所以“不便宜”是“好货”的必要条件，
故选：B．
根据互为逆否命题的真假一致得到：“好货不便宜”是真命题．
所以“好货”⇒“不便宜”，
所以“不便宜”是“好货”的必要条件，
故选：B．
点评：本题考查了必要条件、充分条件与充要条件的判断，属于基础题．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
从5双不同颜色的手套中任取4只，其中恰好有一双同色的取法有（ ）
| A、120 | B、240 |
| C、360 | D、72 |
已知集合A={x|m+1≤x≤2m}，B={x|log2x≤3}，当A∩B=∅时，实数m的取值范围是（ ）
| A、1＜m＜7 |
| B、m＜1或m＞7 |
| C、0≤m＜7 |
| D、m≤0或m＞7 |
如果执行如图所示的程序框图，输入正整数N（N≥2）和实数a1，a2，…，an，输出A，B，则（ ）
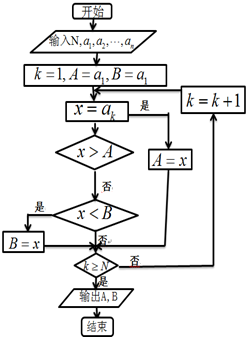
| A、A和B分别是a1，a2，…，an中最小的数和最大的数 | ||
| B、A和B分别是a1，a2，…，an中最大的数和最小的数 | ||
C、
| ||
| D、A+B为a1，a2，…，an的和 |
已知α，β∈R，设p：α＞β，设q：α-sinβcosα＞β-sinαcosβ，则p是q的（ ）
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |