题目内容
已知数列{an}中，a1=1，an=2an-1+2n+3，求{an}的通项公式．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：把给出的递推式两边同时乘以
，然后分别取n=1，2，3，…，n，然后利用累加法求解．
| 1 |
| 2n |
解答：
解：由an=2an-1+2n+3，得：
=
+
+1（n≥2）．
则
=
+
+1，
=
+
+1，
=
+
+1，
…
=
+
+1．
累加得：
=
+3(
+
+…+
)+n-1，
∴
=
+3×
+n-1，
则an=(n+1)•2n-3．
| an |
| 2n |
| an-1 |
| 2n-1 |
| 3 |
| 2n |
则
| a2 |
| 22 |
| a1 |
| 21 |
| 3 |
| 22 |
| a3 |
| 23 |
| a2 |
| 22 |
| 3 |
| 23 |
| a4 |
| 24 |
| a3 |
| 23 |
| 3 |
| 24 |
…
| an |
| 2n |
| an-1 |
| 2n-1 |
| 3 |
| 2n |
累加得：
| an |
| 2n |
| a1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
∴
| an |
| 2n |
| 1 |
| 2 |
| ||||
1-
|
则an=(n+1)•2n-3．
点评：本题考查了数列递推式，考查了累加法求数列的通项公式，考查了等比数列的前n项和，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
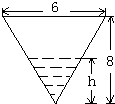将水注入锥形容器中，其速度为4m3/min，设锥形容器的高为8m，顶口直径为6m，求当水深为5m时，水面上升的速度．