题目内容
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:原式各项中的角度变形后,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果.
解答:
解:原式=cos(2π+
)-tan(π+
)+sin(20π+π)=cos
-tan
+sinπ=
-
.
故选:A.
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| ||
| 2 |
| ||
| 2 |
故选:A.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知函数f(x)=sin(ωx+
)(ω>0),若存在实数x0使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2013)成立,则ω的最小值是( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sinxcosy=
,则cosxsiny的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1,1] |
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知平面向量
,
满足|
|=1,|
|=2,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
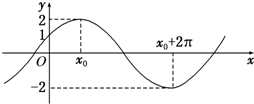 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<