题目内容
如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:设圆柱的底面半径为r,高为h,则4r+2h=4,即2r+h=2,利用基本不等式,可求圆柱体积的最大值.
解答:
解:设圆柱的底面半径为r,高为h,则4r+2h=4,即2r+h=2,
∴2r+h=r+r+h≥3
,∴r2h≤(
)3,
∴V=πr2h≤
π,
∴圆柱体积的最大值为
π,
故选:A.
∴2r+h=r+r+h≥3
| 3 | r2h |
| 2 |
| 3 |
∴V=πr2h≤
| 8 |
| 27 |
∴圆柱体积的最大值为
| 8 |
| 27 |
故选:A.
点评:本题考查圆柱的体积,考查基本不等式的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
将-330°化为弧度为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
下列命题正确的是( )
A、若
| ||||||||
B、若
| ||||||||
C、向量
| ||||||||
| D、两向量相等的充要条件是它们的始点、终点相同 |
已知集合A={x|m+1≤x≤2m},B={x|log2x≤3},当A∩B=∅时,实数m的取值范围是( )
| A、1<m<7 |
| B、m<1或m>7 |
| C、0≤m<7 |
| D、m≤0或m>7 |
已知sinxcosy=
,则cosxsiny的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1,1] |
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,an,输出A,B,则( )
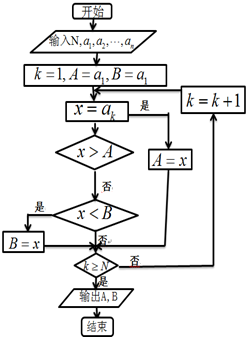

| A、A和B分别是a1,a2,…,an中最小的数和最大的数 | ||
| B、A和B分别是a1,a2,…,an中最大的数和最小的数 | ||
C、
| ||
| D、A+B为a1,a2,…,an的和 |