题目内容
11．在△ABC中，a：b：c=2：4：3，则△ABC中最大角的余弦值是$-\frac{1}{4}$．分析 根据三边之比表示出a，b，c，得到b对的角最大，利用余弦定理即可求出cosB的值．
解答 解：根据题意得：a=2k，b=4k，c=3k，（k＞0）且最大角为B，
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{4{k}^{2}+9{k}^{2}-16{k}^{2}}{12{k}^{2}}$=-$\frac{1}{4}$．
故答案为：-$\frac{1}{4}$．
点评 此题考查了余弦定理在解三角形中的应用，熟练掌握余弦定理是解本题的关键，属于基础题．
练习册系列答案
星级口算天天练系列答案
相关题目
2．椭圆的焦距为8，且椭圆上的点到两个焦点距离之和为10，则该椭圆的标准方程是 （ ）
| A． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B． | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1或$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | ||
| C． | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1 | D． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1或$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1 |
19．在区间[-4，4]上随机地取一个数a，则事件“对任意的正实数x，使x2-ax+1≥0成立”发生的概率为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
3．设$\overrightarrow a$，$\overrightarrow b$是两个不共线向量，且向量$\overrightarrow a+λ\overrightarrow b$与$-\overrightarrow b+2\overrightarrow a$共线，则λ=（ ）
| A． | 0 | B． | $-\frac{1}{2}$ | C． | -2 | D． | $\frac{1}{2}$ |
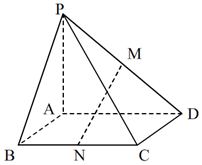如图，在PA⊥面ABCD，面ABCD为矩形，M为PD中点，N为BC中点，