题目内容
17.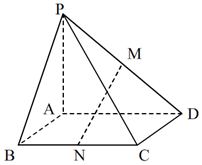 如图,在PA⊥面ABCD,面ABCD为矩形,M为PD中点,N为BC中点,
如图,在PA⊥面ABCD,面ABCD为矩形,M为PD中点,N为BC中点,(1)求证:BC⊥面PAB
(2)求证:MN∥面PAB.
分析 (1)推导出BC⊥PA,BC⊥AB,由此能证明BC⊥平面PAB.
(2)取AD中点G,连结MG、NG,推导出平面MNG∥平面PAB,由此能证明MN∥面PAB.
解答 证明:(1)∵PA⊥面ABCD,BC?平面ABCD,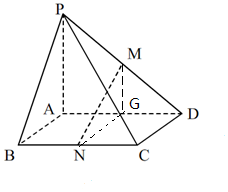
∴BC⊥PA,
∵面ABCD为矩形,∴BC⊥AB,
∵PA∩AB=A,∴BC⊥平面PAB.
(2)取AD中点G,连结MG、NG,
∵M为PD中点,N为BC中点,
∴MG∥PA,NG∥AB,
∵MG∩NG=G,AB∩AP=A,
MG、NG?平面MNG,PA、AB?平面PAB,
∴平面MNG∥平面PAB,
∵MN?平面MNG,∴MN∥面PAB.
点评 本题考查线面垂直、线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.已知点A(2,-3),B(-3,-2),直线m过P(1,1),且与线段AB相交,求直线m的斜率k的取值范围为( )
| A. | $k≥\frac{3}{4}或k≤-4$ | B. | $k≥\frac{3}{4}或k≤-\frac{1}{4}$ | C. | -4≤k≤$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤4 |
2.直线l1:Ax+By+C1=0关于直线l2:Ax+By+C2=0(C1≠C2)对称的直线方程是( )
| A. | Ax+By+(C1-2C2)=0 | B. | Ax+By+(C2-2C1)=0 | C. | Ax+By+(2C2-C1)=0 | D. | Ax+By+(2C1-C2)=0 |
8.已知AD与BC是四面体ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是( )
| A. | $18\sqrt{2}$ | B. | $36\sqrt{2}$ | C. | 18 | D. | 36 |
4.已知集合A={x|(x+2)(x-3)≤0,x∈Z},B={x|(x+1)(x-1)(x-3)=0},则A∩B=( )
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
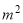 的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左右两侧与后侧内墙各保留1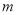 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3