题目内容
7.不等式|x+1|-|x-2|>1的解集为(1,+∞).分析 通过对x分类讨论①当x>2时,②当-1≤x≤2时,③当x<-1时,去掉绝对值符号即可得出.
解答 解:①当x>2时,不等式|x+1|-|x-2|>1可化为x+1-x+2>1,恒成立;
②当-1≤x≤2时,原不等式可化为x+1+x-2>1,解得x>1,∴1<x≤2;
③当x<-1时,原不等式可化为-x-1+x-2>1,无解.
综上可知:原不等式的解集为(1,+∞).
故答案为(1,+∞).
点评 熟练掌握分类讨论思想方法是解含绝对值的不等式的常用方法之一.

练习册系列答案
相关题目
17.已知全集U={x|x≤9,x∈N+},集合A={1,2,3},B={3,4,5,6},则∁U(A∪B)=( )
| A. | {3} | B. | {7,8} | C. | {7,8,9} | D. | {1,2,3,4,5,6} |
18.曲线y=x2-1与直线y=2x+2轴围成的封闭部分的面积为( )
| A. | $\frac{17}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
2.已知直线l与椭圆C:$\frac{x^2}{4}+{y^2}=1$交于A,B两点,且|AB|=2,则直线l与圆x2+y2=1的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相交或相切 |
19.已知某几何体的三视图如图所示,则该几何体的体积为( )
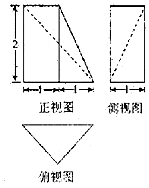

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |