题目内容
2.已知直线l与椭圆C:$\frac{x^2}{4}+{y^2}=1$交于A,B两点,且|AB|=2,则直线l与圆x2+y2=1的位置关系为( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相交或相切 |
分析 画出椭圆与圆的图形,通过线段AB的距离,判断位置关系即可.
解答 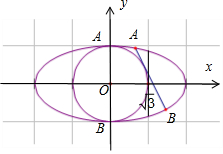 解:椭圆C:$\frac{x^2}{4}+{y^2}=1$与圆x2+y2=1的图形如图,AB的距离为2,显然AB是椭圆的短轴长时,直线l与椭圆相交,椭圆的通经长为:$\sqrt{3}$,
解:椭圆C:$\frac{x^2}{4}+{y^2}=1$与圆x2+y2=1的图形如图,AB的距离为2,显然AB是椭圆的短轴长时,直线l与椭圆相交,椭圆的通经长为:$\sqrt{3}$,
在图形中存在|AB|=2,直线l与圆相切,设直线l:y=kx+m,由题意可得:$\frac{|m|}{\sqrt{1+{k}^{2}}}=1$…①,$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y整理可得(1+4k2)x2+8kmx+4m2-4=0,可得x1+x2=$\frac{-8mk}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}|{x}_{2}-{x}_{1}|$=2,代入x1+x2,x1x2,化简整理可得:$\frac{2\sqrt{1+{k}^{2}}}{1+4{k}^{2}}\sqrt{4{k}^{2}-{m}^{2}+1}=1$…②
联立①②消去m可得:$\frac{2\sqrt{1+{k}^{2}}}{1+4{k}^{2}}\sqrt{3{k}^{2}}=1$,化简可得:4k4-4k2+1=0,解得k=$±\frac{\sqrt{2}}{2}$,
所以转化的直线l存在,由4条.
所以直线与圆的位置关系是相交或相切.
故选:D.
点评 本题考查椭圆的简单性质以及圆的图形的应用,考查数形结合分析问题解决问题的能力.

练习册系列答案
相关题目
12.已知等差数列{an}的公差为d,等比数列{bn}的公比为q,设{an},{bn}的前n项和分别为Sn,Tn,若${n^2}({T_n}+1)={2^n}{S_n}$,n∈N*,则d=2,q=2.
10.已知集合A={-1,0,1},B={x|x=sin$\frac{2k+1}{x}$,k∈Z},则∁AB=( )
| A. | ∅ | B. | 0 | C. | {0} | D. | {-1,1} |
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).