题目内容

19．已知某几何体的三视图如图所示，则该几何体的体积为（　　）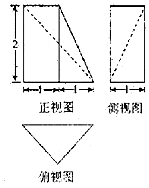
A．$\frac{2}{3}$B．$\frac{4}{3}$C．2D．$\frac{8}{3}$

分析 如图所示，该几何体为：多面体DE-ABC．CE⊥底面ABC，DA⊥底面ABC．ADEC为矩形．△ABC为等腰直角三角形，BC=2，AC⊥AB．连接AE，该几何体的体积V=VE-ABC+VB-ADE，即可得出．

解答 解：如图所示，该几何体为：多面体DE-ABC．CE⊥底面ABC，DA⊥底面ABC．ADEC为矩形．
△ABC为等腰直角三角形，BC=2，AC⊥AB．
连接AE，该几何体的体积V=VE-ABC+VB-ADE
=$\frac{1}{3}×\frac{1}{2}×1×2×2$+$\frac{1}{3}×\frac{1}{2}×{2}^{2}×1$=$\frac{4}{3}$．
故选：B．

点评 本题考查了三棱锥的三视图与体积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
9．已知函数f（x）=x-alnx（a∈R）．
（1）若曲线y=f（x）在x=1处的切线与直线x-2y-7=0垂直，求f（x）的单调区间；
（2）求证：f（x）≥1恒成立的充要条件是a=1．
10．已知集合A={-1，0，1}，B={x|x=sin$\frac{2k+1}{x}$，k∈Z}，则∁AB=（　　）
A．∅B．0C．{0}D．{-1，1}
7．不等式|x+1|-|x-2|＞1的解集为（1，+∞）．
14．f（x）=$\sqrt{{x}^{2}+2x+1}$，g（x）=|x-1|．
（1）求不等式|f（x）-1|＜2的解集；
（2）当|a+b|-|a-b|＞2|b|[f（x）-g（x）]（b≠0，a，b∈R）的解集非空，求x的取值范围．
4．已知焦距为2$\sqrt{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点为A，直线y=$\frac{4}{3}$与椭圆C交于P、Q两点（P在Q的左边），Q在x轴上的射影为B，且四边形ABPQ是平行四边形．
（1）求椭圆C的方程；
（2）斜率为k的直线l与椭圆C交于两个不同的点M，N．
（i）若直线l过原点且与坐标轴不重合，E是直线3x+3y-2=0上一点，且△EMN是以E为直角顶点的等腰直角三角形，求k的值
（ii）若M是椭圆的左顶点，D是直线MN上一点，且DA⊥AM，点G是x轴上异于点M的点，且以DN为直径的圆恒过直线AN和DG的交点，求证：点G是定点．
11．如图，一张A4纸的长、宽分别为2$\sqrt{2}$a，2a，A，B，C，D分别是其四条边的中点，现将其沿图中虚线折起，使得P1，P2，P3，P4四点重合为一点P，从而得到一个多面体，关于该多面体的下列命题，正确的是①②③④．（写出所有正确命题的序号）．
①该多面体是三棱锥；②平面BAD⊥平面BCD；
③平面BAC⊥平面ACD；④该多面体外接球的表面积为5πa2．
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，右顶点为A，下顶点为B，点P（$\frac{3}{4}$，0）满足|PA|=|PB|．
（Ⅰ）求椭圆C的方程．
（Ⅱ）不垂直于坐标轴的直线l与椭圆C交于M，N两点，以MN为直径的圆过原点，且线段MN的垂直平分线过点P，求直线l的方程．
9．已知椭圆Γ的左、右焦点分别为F1（-1，0）、F2（1，0）．经过点F1且倾斜角为θ（0＜θ＜π）的直线l与椭圆Γ交于A、B两点（其中点A在x轴上方），△ABF2的周长为8．
（1）求椭圆Γ的标准方程；
（2）如图，把平面xOy沿x轴折起来，使y轴正半轴和x轴确定的半平面，与y负半轴和x轴所确定的半平面互相垂直．
①若θ=$\frac{π}{3}$，求异面直线AF1和BF2所成角的大小；
②若折叠后△ABF2的周长为$\frac{15}{2}$，求θ的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网