题目内容
16.已知函数f(x)=$\sqrt{|x+1|+|x-3|-m}$的定义域为R.(Ⅰ)求m的取值范围;
(Ⅱ)若m的最大值为n,解关于x的不等式:|x-3|-2x≤2n-4.
分析 (Ⅰ)由题意,|x+1|+|x-3|-m≥0恒成立,利用基本不等式,可得求m的取值范围;
(Ⅱ)m的最大值为4,关于x的不等式:|x-3|-2x≤4,分类讨论,即可解关于x的不等式.
解答 解:(Ⅰ)由题意,|x+1|+|x-3|-m≥0恒成立.
∵|x+1|+|x-3|≥|(x+1)-)x-3)|=4,
∴m≤4;
(Ⅱ)m的最大值为4,关于x的不等式:|x-3|-2x≤4.
∴$\left\{\begin{array}{l}{x≥3}\\{x-3-2x≤4}\end{array}\right.$或$\left\{\begin{array}{l}{x<3}\\{3-x-2x≤4}\end{array}\right.$,
∴x≥3或-$\frac{1}{3}$≤x<3,
∴不等式的解集为{x|x≥-$\frac{1}{3}$}.
点评 本题考查恒成立问题,考查绝对值不等式的解法,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
6.设正三棱锥A-BCD(底面是正三角形,顶点在底面的射影为底面中心)的所有顶点都在球O的球面上,BC=2,E,F分别是AB,BC的中点,EF⊥DE,则球O的表面积为( )
| A. | $\frac{3π}{2}$ | B. | 6π | C. | 8π | D. | 12π |
6.如图为某几何体的三视图,则该几何体的外接球的直径为( )
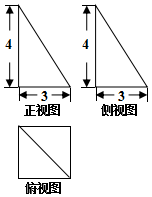

| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).