题目内容

18．曲线y=x2-1与直线y=2x+2轴围成的封闭部分的面积为（　　）
A．$\frac{17}{3}$B．$\frac{22}{3}$C．$\frac{32}{3}$D．$\frac{35}{3}$

分析 联立方程组求出积分的上限和下限，结合积分的几何意义即可得到结论．

解答 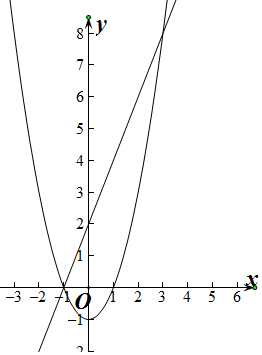解：作出两条曲线对应的封闭区域如图：
由$\left\{\begin{array}{l}{y={x}^{2}-1}\\{y=2x+2}\end{array}\right.$得x2=x+2，即x2-x-2=0，
解得x=-1或x=3，
则根据积分的几何意义可知所求的几何面积
S=${∫}_{-1}^{3}$[2x+2-（x2-1）]dx=S=${∫}_{-1}^{3}$（2x+3-x2-1）dx
=（x2+3x-$\frac{1}{3}$x3）|${\;}_{-1}^{3}$=（9+9-9）-（1-3+$\frac{1}{3}$）=$\frac{32}{3}$，
故选：C

点评 本题主要考查积分的应用，作出对应的图象，求出积分上限和下限，是解决本题的关键．

练习册系列答案
相关题目
8．已知数列{an}满足an+1=an+3，a1=0，则数列{an}的通项公式可以是（　　）
A．nB．2nC．3n-3D．3n+3
9．已知函数f（x）=x-alnx（a∈R）．
（1）若曲线y=f（x）在x=1处的切线与直线x-2y-7=0垂直，求f（x）的单调区间；
（2）求证：f（x）≥1恒成立的充要条件是a=1．
6．设正三棱锥A-BCD（底面是正三角形，顶点在底面的射影为底面中心）的所有顶点都在球O的球面上，BC=2，E，F分别是AB，BC的中点，EF⊥DE，则球O的表面积为（　　）
A．$\frac{3π}{2}$B．6πC．8πD．12π
13．已知函数f（x）=（x-a）e-x，其中a为常数．
（1）判断f（x）在x=0处的切线是否经过一个定点，并说明理由；
（2）讨论f（x）在区间[-2，3]上的单调性．
3．三棱锥V-ABC的三条棱VA，VB，VC两两垂直，三个侧面与底面所成的二面角大小分别为α，β，γ．求证：$cosαcosβcosγ（{\frac{1}{{{{cos}^2}α}}+\frac{1}{{{{cos}^2}β}}+\frac{1}{{{{cos}^2}γ}}}）≥\sqrt{3}$．
10．已知集合A={-1，0，1}，B={x|x=sin$\frac{2k+1}{x}$，k∈Z}，则∁AB=（　　）
A．∅B．0C．{0}D．{-1，1}
7．不等式|x+1|-|x-2|＞1的解集为（1，+∞）．
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，右顶点为A，下顶点为B，点P（$\frac{3}{4}$，0）满足|PA|=|PB|．
（Ⅰ）求椭圆C的方程．
（Ⅱ）不垂直于坐标轴的直线l与椭圆C交于M，N两点，以MN为直径的圆过原点，且线段MN的垂直平分线过点P，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网