题目内容
12．设函数f（x）=|x-1|-|2x+1|的最大值为m．（1）作出函数f（x）的图象；
（2）若a2+2c2+3b2=m，求ab+2bc的最大值．
分析 （1）分类讨论，作出函数f（x）的图象；
（2）求出函数的值域，即可求m的值，利用基本不等式求ab+2bc的最大值．
解答 解：（1）当x≤-$\frac{1}{2}$时，f（x）=（1-x）+2x+1=x+2；
当-$\frac{1}{2}$＜x＜1时，f（x）=（1-x）-2x-1=-3x：
当x≥1时，f（x）=（x-1）-2x-1=-x-2，
函数f（x）的图象，如图所示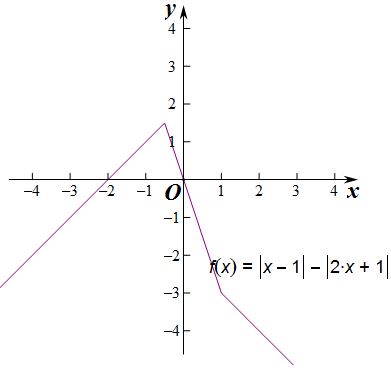
；
（2）由题意，当x=-$\frac{1}{2}$时，f（x）取得最大值m=1.5，∴a2+2c2+3b2=1.5，
∴ab+2bc≤$\frac{1}{2}$（a2+2c2+3b2）=$\frac{3}{4}$，即ab+2bc的最大值为$\frac{3}{4}$．
点评 本题考查绝对值不等式，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
20．
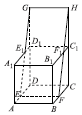如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）
如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）| A． | $\frac{\sqrt{19}a}{3}$ | B． | $\frac{\sqrt{19}a}{9}$ | C． | $\frac{\sqrt{2}a}{3}$ | D． | $\frac{\sqrt{2}a}{9}$ |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同，F1，F2为椭圆的左、右焦点．M为椭圆上任意一点，△MF1F2面积的最大值为4$\sqrt{2}$．
如图，正方体ABCD-A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM=BN≠$\sqrt{2}$，有以下四个结论：①AA1⊥MN；②AB∥MN；③MN∥平面A1B1C1D1；④MN与A1C1一定是异面直线．其中正确命题的序号是（ ）