题目内容
17.已知函数$f(x)=a-\frac{1}{|x|}(a≠0)$.(1)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围;
(2)若函数y=f(x)在[m,n]上的值域是[m,n],求实数a的取值范围.
分析 (1)由f(x)<2x在(1,+∞)上恒成立,得a<$\frac{1}{x}$+2x.记g(x)=$\frac{1}{x}$+2x,在(1,+∞)上是增函数,得g(x)>g(1)=3,由此能求出a的范围.
(2)函数y=f(x)的定义域为(-∞,0)∪(0,+∞),再由n>m>0和0>n>m两种情况分别讨论实数a的取值范围.
解答 解:(1)若f(x)<2x在(1,+∞)上恒成立,
得a-$\frac{1}{x}$<2x即a<$\frac{1}{x}$+2x,
记g(x)=$\frac{1}{x}$+2x,在(1,+∞)上是增函数,
得g(x)>g(1)=3,
所以:a≤3
(2)函数y=f(x)的定义域为(-∞,0)∪(0,+∞)
ⅰ)当n>m>0时,f(x)在[m,n]上是增函数,
故$\left\{\begin{array}{l}{f(m)=m}\\{f(n)=n}\end{array}\right.$,解得:a>2;
ⅱ) 当0>n>m时,f(x)在[m,n]上是减函数,
故$\left\{\begin{array}{l}{f(m)=n}\\{f(n)=m}\end{array}\right.$,解得:a=0;
所以:a∈{0}∪(2,+∞).
点评 本题考查函数的单调性质的应用,解题时要认真审题,仔细求解,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )| A. | ①③ | B. | ②③ | C. | ①④ | D. | ①③④ |
6.如图为某几何体的三视图,则该几何体的外接球的直径为( )
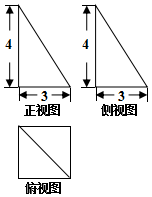

| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
7.某几何体的三视图如图所示,在该几何体的体积是( )
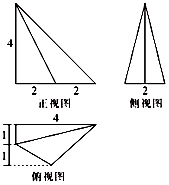

| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
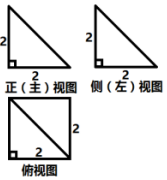
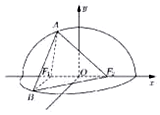 已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.
已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.