题目内容
已知点A（-1，-2，1），B（2，2，2），点P在Z轴上，且点P到A，B的距离相等，则点P的坐标为 ．
考点：空间向量的夹角与距离求解公式
专题：空间位置关系与距离
分析：设P（0，0，z）．由于点P到A，B的距离相等，可得
=
，解出即可．
| 12+22+(z-1)2 |
| 22+22+(2-z)2 |
解答：
解：设P（0，0，z）．
∵点P到A，B的距离相等，
∴
=
，
化为2z=6，解得z=3．
∴点P的坐标（0，0，3）．
故答案为：（0，0，3）．
∵点P到A，B的距离相等，
∴
| 12+22+(z-1)2 |
| 22+22+(2-z)2 |
化为2z=6，解得z=3．
∴点P的坐标（0，0，3）．
故答案为：（0，0，3）．
点评：本题考查了两点之间的距离公式，属于基础题．
练习册系列答案
相关题目
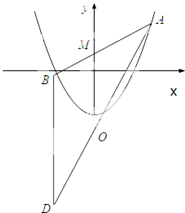如图，已知抛线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）．
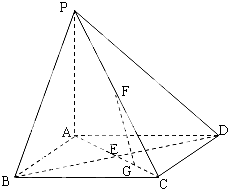如图，在底面是正方形的四棱锥P-ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为EC中点．