Question

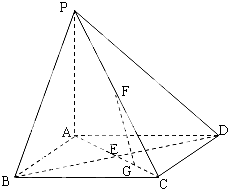如图，在底面是正方形的四棱锥P-ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为EC中点．
（1）求证：FG∥平面PBD；
（2）当二面角B-PC-D的大小为

2π

3

时，求FG与平面PCD所成角的正切值．

Answer 1

考点：直线与平面所成的角,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）直接利用直线与平面平行的判定定理证明FG∥平面PBD；
（2）以AB为x轴，AD为y 轴，AP为z轴，建立如图空间直角坐标系．设AB=1，AP=t 推出B，C，D，P，相关点的坐标，利用二面角B-PC-D的大小为

2π

3

，通过FG对应向量以及平面PCD的法向量，利用数量积，即可求解的正切值．

解答： （本小题满分14分）．
解：（1）连接PE，G．、F为EC和PC的中点，∴FG∥PE，FG?平面PBD，PE?平面PBD，∴FG∥平面PBD…（5分）
（2）以AB为x轴，AD为y 轴，AP为z轴，建立如图空间直角坐标系．
设AB=1，AP=t 则B（1，0，0），C（1，1，0），D（0，1，0），P（0，0，t），F(

1

2

，

1

2

，

t

2

)，G(

3

4

，

3

4

，0)…（7分）
∴

BP

=(-1，0，t)，

BC

=(0，1，0)，∴平面BPC的一个法向量为

n

=(t，0，1)
又

DC

=(1，0，0)，

DP

=(0，-1，t)，∴平面DPC的一个法向量为

m

=(0，t，1)…（9分）
∵二面角B-PC-D的大小为

2π

3

，∴|cos＜

n

，

m

＞|=|

1

t2+1

|=

1

2

∴t=1…（11分）
∴

FG

=(

1

4

，

1

4

，-

1

2

)
∴FG与平面PCD所成角θ的正弦值sinθ=|

1 4 - 1 2

1 16 + 1 16 + 1 4 • 2

|=

3

6

，…（13分）
∴tanθ=

11

11

…（14分）

点评：本题考查空间向量的水力计算的应用，直线与平面所成角，二面角的应用，直线与平面平行的判定定理的应用，考查科空间想象能力以及计算能力．