题目内容
已知二次函数f(x)的图象顶点为A(0,15),且图象在x轴上截得线段长为8.
(1)求函数f(x)的解析式;
(2)证明:函数f(x)在(1,+∞)上是减函数
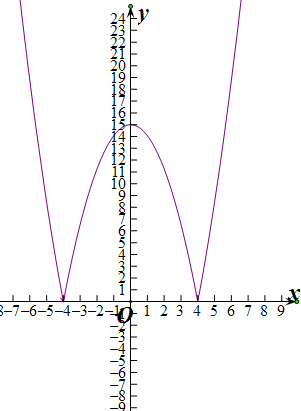
(3)若g(x)=|f(x)|,试画出函数g(x)的图象(只画草图).
(1)求函数f(x)的解析式;
(2)证明:函数f(x)在(1,+∞)上是减函数
(3)若g(x)=|f(x)|,试画出函数g(x)的图象(只画草图).
考点:二次函数的性质,函数的图象
专题:函数的性质及应用
分析:(1)根据题意设出函数式子f(x)=a(x-4)(x+4)=a(x2-16),利用A(0,15)求解即可.(2)根据单调性定义作差证明.(3)画出函数图象判断即可.
解答:
解:(1)∵二次函数f(x)的图象顶点为A(0,15),且图象在x轴上截得线段长为8.
∴设f(x)=a(x-4)(x+4)=a(x2-16),f(0)=15,
∴a=-
,
∴f(x)=-
x2+15,
(2)∵设1<x1<x2,f(x1)=-
x12+15,f(x2)=-
x22+15,
∴f(x1)-f(x2)=-
(x1+x2)(x1-x2),
∵x1+x2>2,x1-x2<0
∴
(x1+x2)(x1-x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(1,+∞)上是减函数
(3)g(x)=|f(x)|,
∴设f(x)=a(x-4)(x+4)=a(x2-16),f(0)=15,
∴a=-
| 15 |
| 16 |
∴f(x)=-
| 15 |
| 16 |
(2)∵设1<x1<x2,f(x1)=-
| 15 |
| 16 |
| 15 |
| 16 |
∴f(x1)-f(x2)=-
| 15 |
| 16 |
∵x1+x2>2,x1-x2<0
∴
| 15 |
| 16 |
∴f(x1)>f(x2),
∴函数f(x)在(1,+∞)上是减函数
(3)g(x)=|f(x)|,

点评:本题考查了二次函数的性质,解析式的特征,待定系数思想,画函数的图象,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
一个三角形用斜二测画法所作的直观图是一个边长为1正三角形,则原三角形的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
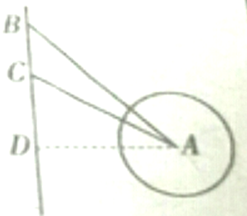 某学校组织同学们参加红色七日游--还上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只正向南航行,在B处测得小岛A在船的南偏东30°;航行30海里后,在C处测得小岛A在船的南偏东60°,如果此船不改变航向,继续向南航行,有无触礁危险?
某学校组织同学们参加红色七日游--还上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只正向南航行,在B处测得小岛A在船的南偏东30°;航行30海里后,在C处测得小岛A在船的南偏东60°,如果此船不改变航向,继续向南航行,有无触礁危险? 已知A(-2,0),B(2,0)为坐标平面上两个定点,动点M在x轴上的射影为N,且满足|MN|2=4|AN|•|BN|.
已知A(-2,0),B(2,0)为坐标平面上两个定点,动点M在x轴上的射影为N,且满足|MN|2=4|AN|•|BN|.