题目内容
已知集合A={(x,y)|x(x-1)+y(y-1)≤r},集合B={(x,y)|x2+y2≤r2},若A⊆B,则r的取值范围为 .
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:若由题意,A,B表示的圆内切或内含,由圆心距与半径之间的关系,构造关于r的不等式,解不等式即可得到实数r的取值范围.
解答:
解:若由题意,A,B表示的圆内切或内含
由于A中的圆的圆心为N(
,
),半径为
,
B中的圆的圆心为M(0,0),半径为r,
则r-
≥|MN|=
,
∴r≥
+1,
故答案为:r≥
+1.
由于A中的圆的圆心为N(
| 1 |
| 2 |
| 1 |
| 2 |
r+
|
B中的圆的圆心为M(0,0),半径为r,
则r-
r+
|
| ||
| 2 |
∴r≥
| 2 |
故答案为:r≥
| 2 |
点评:本题考查的知识点是圆与圆的位置关系及其判定,其中根据集合之间的关系,转化为圆与圆的位置关系,进而转化为圆心距与半径差之间的关系,是解答本题的关键.

练习册系列答案
相关题目
已知等比数列{an}满足a2=2,a4a6=4a72,则a4的值为( )
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
如图Rt△O′A′B′是一平面图形的直观图,直角边O′B′=2,则这个平面图形的面积是( )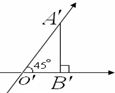

A、2
| ||
| B、1 | ||
C、4
| ||
D、
|