题目内容
已知f是从数集a到b的一一映射,若a中有三个元素,则b的非空真子集的个数是 .
考点:子集与真子集
专题:计算题,函数的性质及应用,集合
分析:由一一映射可知,a中的元素个数与b中的相同,对于有限集合,我们有以下结论:若一个集合中有n个元素,则它有2n个子集.
解答:
解:∵f是从数集a到b的一一映射,且a中有三个元素,
∴b中也有三个元素,
∴b的非空真子集的个数是23-2=6,
故答案为:6.
∴b中也有三个元素,
∴b的非空真子集的个数是23-2=6,
故答案为:6.
点评:本题考查了一一映射的概念及集合的子集个数,若一个集合中有n个元素,则它有2n个子集,有(2n-1)个真子集,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知某个几何体的三视图如右图,根据图中标出的尺寸可得这个几何体的体积是( )
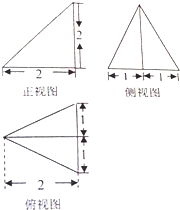

A、
| ||
B、
| ||
C、
| ||
D、
|
设a>0,且a≠1,且a≠2,则“函数y=logax在(0,+∞)上是减函数”是“函数y=(a-2)ax在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后关于y轴对称,则y=f(x)对应的解析式为 ( )
| π |
| 2 |
| π |
| 3 |
A、y=sin(2x-
| ||
B、y=cos(2x+
| ||
C、y=cos(2x-
| ||
D、y=sin(2x+
|
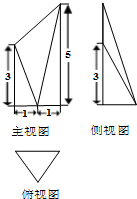 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为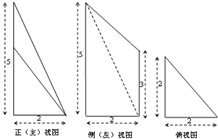
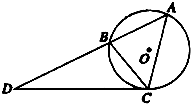 如图所示,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=
如图所示,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=