题目内容
已知函数f(x)=loga(1-x)+loga(x+3),0<a<1,若函数f(x)的最小值为-4,求a的值.
考点:对数的运算性质
专题:计算题,函数的性质及应用
分析:由题意,
,从而求出函数的定义域{x|-3<x<1},化简f(x)=loga(1-x)(x+3),由0<a<1可得f(-1)=loga4=-4,从而解a.
|
解答:
解:由题意,
,
解得,-3<x<1,
则f(x)=loga(1-x)+loga(x+3)
=loga(1-x)(x+3),
又∵0<a<1,
∴f(-1)=loga4=-4,
则a=
.
|
解得,-3<x<1,
则f(x)=loga(1-x)+loga(x+3)
=loga(1-x)(x+3),
又∵0<a<1,
∴f(-1)=loga4=-4,
则a=
| ||
| 2 |
点评:本题考查了函数的定义域的求法及对数函数的单调性的应用,属于基础题.

练习册系列答案
相关题目
在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
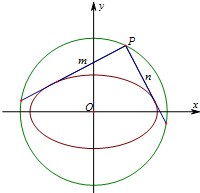 椭圆C的中心在原点,焦点在x轴上,离心率为
椭圆C的中心在原点,焦点在x轴上,离心率为
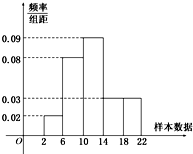 如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.