题目内容
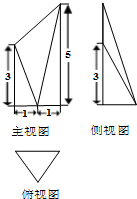 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,判断几何体的形状是底面为正三角形,两条侧棱垂直底面的几何体,结合数据求出该几何体的体积.
解答:
 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是底面为正三角形,两条侧棱垂直底面的几何体,如图所示;
该几何体也是底面为直角梯形,高为2×
=
的四棱锥;
∴它的体积是V四棱锥=
×(3+5)×2×
×
=
.
故答案为:
.
 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;该几何体是底面为正三角形,两条侧棱垂直底面的几何体,如图所示;
该几何体也是底面为直角梯形,高为2×
| ||
| 2 |
| 3 |
∴它的体积是V四棱锥=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
8
| ||
| 3 |
故答案为:
8
| ||
| 3 |
点评:本题考查了三视图的应用问题,解题时应根据几何体的三视图,得出几何体的形状是什么,是基础题.

练习册系列答案
相关题目
在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
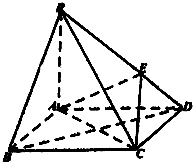 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=