题目内容
P是双曲线C：
-
=1（a，b＞0）上的一点，C的半焦距为c，M，N分别是圆（x+c）2+y2=（c-a）2，（x-c）2+y2=（c-a）2上的点，若|PM|-|PN|的最大值为4a，则C的离心率为 ．
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：由题设通过双曲线的定义推出|PF1|-|PF2|=6，利用|MP|≤|PF1|+|MF1|，|PN|≥|PF2|-|NF2|，推出|PM|-|PN|≤|PF1|+|MF1|-|PF2|-|NF2|，求出最大值．
解答：
解：双曲线双曲线C：
-
=1（a，b＞0）中，如图
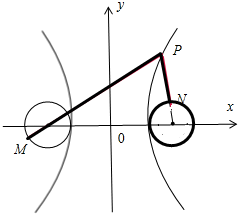
∴F1（-c，0），F2（c，0），
∵|PF1|-|PF2|=2a，
∴|MP|≤|PF1|+|MF1|，|PN|≥|PF2|-|NF2|，
∴-|PN|≤-|PF2|+|NF2|，
所以，|PM|-|PN|≤|PF1|+|MF1|-|PF2|+|NF2|=2a+c-a+c-a=4a，
即c=2a，
所以C的离心率为2；
故答案为：2
| x2 |
| a2 |
| y2 |
| b2 |
∴F1（-c，0），F2（c，0），
∵|PF1|-|PF2|=2a，
∴|MP|≤|PF1|+|MF1|，|PN|≥|PF2|-|NF2|，
∴-|PN|≤-|PF2|+|NF2|，
所以，|PM|-|PN|≤|PF1|+|MF1|-|PF2|+|NF2|=2a+c-a+c-a=4a，
即c=2a，
所以C的离心率为2；
故答案为：2
点评：本题主要考查直线与圆锥曲线的综合应用能力，关键时利用双曲线的定义结合三角形的三边关系得到|PM|-|PN|的线段表示；解题时要注意合理地进行等价转化．
练习册系列答案
阅读快车系列答案
相关题目
已知f（x）=2x+3（x∈R），若|f（x）|＜a的必要条件是|x+1|＜b（a，b＞0），则a，b之间的关系是（ ）
A、b≥
| ||
B、b＜
| ||
C、a≤
| ||
D、a＞
|
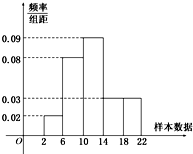如图是学校从走读生中随机调查200名走读生早上上学所需时间（单位：分钟）样本的频率分布直方图．