题目内容
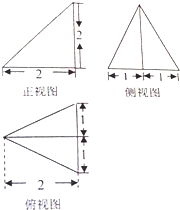
已知某个几何体的三视图如右图，根据图中标出的尺寸可得这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体是一个三棱锥，三棱锥的底面是一个底边是2，高是2的三角形，做出面积是，三棱锥的高是2，根据三棱锥的体积公式得到结果．
解答：
解：由三视图知几何体是一个三棱锥，三棱锥的底面是一个底边是2，高是2的三角形，面积是
×2×2=2
三棱锥的高是2，
∴三棱锥的体积是
×2×2=
故选C．
| 1 |
| 2 |
三棱锥的高是2，
∴三棱锥的体积是
| 1 |
| 3 |
| 4 |
| 3 |
故选C．
点评：本题考查由三视图还原几何体并且看出几何体各个部分的长度，本题解题的关键是要求体积需要求出几何体的底面面积和高．本题是一个基础题．
练习册系列答案
相关题目
已知{an}是等比数列，其中a1，a8是关于x的方程x2-2xsinα-
sinα=0的两根，且（a1+a8）2=2a3a6+6，则锐角α的值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x|x+1＜0}，B={x|x-3＜0}，那么集合A∪B等于（ ）
| A、{x|x＜-3} |
| B、{x|x＜3} |
| C、{x|x＜-1} |
| D、{x|-1＜x＜3} |
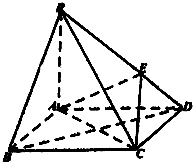如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=
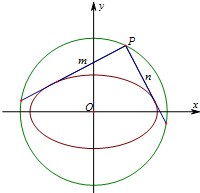椭圆C的中心在原点，焦点在x轴上，离心率为