题目内容
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后关于y轴对称,则y=f(x)对应的解析式为 ( )
| π |
| 2 |
| π |
| 3 |
A、y=sin(2x-
| ||
B、y=cos(2x+
| ||
C、y=cos(2x-
| ||
D、y=sin(2x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由周期求得ω,根据诱导公式以及y=Asin(ωx+φ)的图象变换规律,可得y=f(x)的解析式.
解答:
解:由题意可得
=π,∴ω=2.
把函数f(x)=sin(2x+φ)图象向右平移
个单位后,
所得图象对应的函数解析式为y=sin[2(x-
)+φ]=sin(2x+φ-
),
由于所得函数的图象关于y轴对称,故y=sin(2x+φ-
)为偶函数,
∴φ-
=kπ+
,k∈z,即 φ=kπ+
.
再结合,|φ|<
,可得φ=
,∴f(x)=sin(2x+
)=cos(2x-
),
故选:C.
| 2π |
| ω |
把函数f(x)=sin(2x+φ)图象向右平移
| π |
| 3 |
所得图象对应的函数解析式为y=sin[2(x-
| π |
| 3 |
| 2π |
| 3 |
由于所得函数的图象关于y轴对称,故y=sin(2x+φ-
| 2π |
| 3 |
∴φ-
| 2π |
| 3 |
| π |
| 2 |
| 7π |
| 6 |
再结合,|φ|<
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
故选:C.
点评:本题主要考查诱导公式的应用,利用了y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
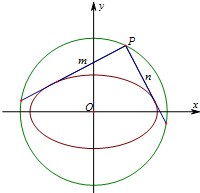 椭圆C的中心在原点,焦点在x轴上,离心率为
椭圆C的中心在原点,焦点在x轴上,离心率为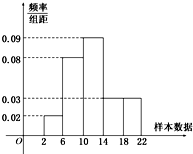 如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.