题目内容
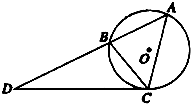如图所示，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=| 15 |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理得BD=3，DA=5，由弦切角定理得△DCB∽△DAC，从而BC•DA=AC•CD，由此能求出AC的长．
解答：
解：∵CD是过点C圆的切线
DBA为圆的割线
由切割线定理得：
CD2=DB•DA
由CD=
，AB=BC=2，
解得BD=3，
∴DA=5，
由弦切角定理可得：∠DCB=∠A，又由∠D=∠D
∴△DCB∽△DAC
∴BC•DA=AC•CD，
由BC=2，DA=5，CD=
，得
AC=
=
．
故答案为：
．
DBA为圆的割线
由切割线定理得：
CD2=DB•DA
由CD=
| 15 |
解得BD=3，
∴DA=5，
由弦切角定理可得：∠DCB=∠A，又由∠D=∠D
∴△DCB∽△DAC
∴BC•DA=AC•CD，
由BC=2，DA=5，CD=
| 15 |
AC=
| 2×5 | ||
|
2
| ||
| 3 |
故答案为：
2
| ||
| 3 |
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意切割线定理、弦切角定理的合理运用．
练习册系列答案
相关题目
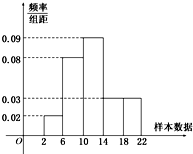如图是学校从走读生中随机调查200名走读生早上上学所需时间（单位：分钟）样本的频率分布直方图．