题目内容
设a>0,且a≠1,且a≠2,则“函数y=logax在(0,+∞)上是减函数”是“函数y=(a-2)ax在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:结合对数函数,指数函数的性质分别证明充分性和必要性,从而得到答案.
解答:
解:∵函数y=logax在(0,+∞)上是减函数,
∴0<a<1,
∴a-2<0,
∴函数y=(a-2)ax在R上是增函数,
故是充分条件;
若函数y=(a-2)ax在R上是增函数,
则:
或
,
解得:a>2或0<a<1,
推不出函数y=logax在(0,+∞)上是减函数,
故不是必要条件,
故选:A.
∴0<a<1,
∴a-2<0,
∴函数y=(a-2)ax在R上是增函数,
故是充分条件;
若函数y=(a-2)ax在R上是增函数,
则:
|
|
解得:a>2或0<a<1,
推不出函数y=logax在(0,+∞)上是减函数,
故不是必要条件,
故选:A.
点评:本题考查了充分本题条件,考查了对数函数,综上函数的性质,是一道基础题.

练习册系列答案
相关题目
已知集合A={x|x+1<0},B={x|x-3<0},那么集合A∪B等于( )
| A、{x|x<-3} |
| B、{x|x<3} |
| C、{x|x<-1} |
| D、{x|-1<x<3} |
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
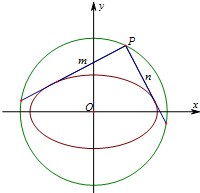 椭圆C的中心在原点,焦点在x轴上,离心率为
椭圆C的中心在原点,焦点在x轴上,离心率为