题目内容
已知f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值,则( )
| A、f(x-1)一定是奇函数 |
| B、f(x-1)一定是偶函数 |
| C、f(x+1)一定是奇函数 |
| D、f(x+1)一定是偶函数 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据三角函数的图象和性质,即可得到结论.
解答:
解:∵函数f(x)在x=1处取最大值,
∴x=1是函数f(x)的一条对称轴,
将函数f(x)向左平移1个单位,得到函数f(x+1)的图象,此时函数关于y轴对称,则函数为偶函数.
故选:D
∴x=1是函数f(x)的一条对称轴,
将函数f(x)向左平移1个单位,得到函数f(x+1)的图象,此时函数关于y轴对称,则函数为偶函数.
故选:D
点评:本题主要考查三角函数的图象和性质,根据函数最值和对称轴之间的关系是解决本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
函数y=x2-x,(-1<x<4)值域是( )
A、[-
| ||
| B、(2,12) | ||
| C、( 2,20) | ||
D、[-
|
如果在约束条件
(0<a<1)下,目标函数x+ay最大值是
,则a=( )
|
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图,当x1=6,x2=9,p=8.5时,x3等于( )
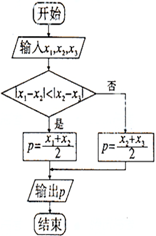

| A、8 | B、4 | C、10 | D、9 |
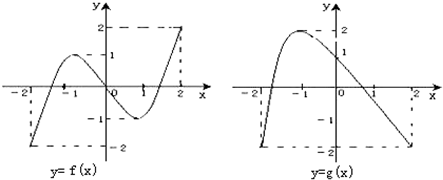
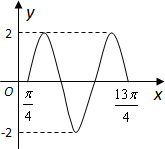 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=