题目内容
已知函数f(x)=a x2-3x-3(a>0,且a≠1),在x∈[1,3]时有最小值
,求a的值及f(x)最大值.
| 1 |
| 8 |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:换元法求解得出y=at,-
≤t≤-3,分类思想求出a的值,再利用单调性求解最大值.
| 21 |
| 4 |
解答:
解:设t(x)=x2-3x-3,x∈[1,3],
对称轴x=
时,t(
)=-
,
t(1)=-5,t(3)=-3,
-
≤t(x)≤-3
∴f(x)=a x2-3x-3(a>0,且a≠1),在x∈[1,3]
即y=at,-
≤t≤-3
∵有最小值
,
∴当0<a<1时,a-3=
,a=
,
f(x)最大值=(
) -
=2
,
当a>1时,a -
=
,a=8
,
f(x)最大值=(8
)-3=8 -
对称轴x=
| 3 |
| 2 |
| 3 |
| 2 |
| 21 |
| 4 |
t(1)=-5,t(3)=-3,
-
| 21 |
| 4 |
∴f(x)=a x2-3x-3(a>0,且a≠1),在x∈[1,3]
即y=at,-
| 21 |
| 4 |
∵有最小值
| 1 |
| 8 |
∴当0<a<1时,a-3=
| 1 |
| 8 |
| 1 |
| 2 |
f(x)最大值=(
| 1 |
| 2 |
| 21 |
| 4 |
| 21 |
| 4 |
当a>1时,a -
| 21 |
| 4 |
| 1 |
| 8 |
| 4 |
| 21 |
f(x)最大值=(8
| 4 |
| 21 |
| 4 |
| 7 |
点评:本题考察了指数函数的性质,分类讨论思想,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值,则( )
| A、f(x-1)一定是奇函数 |
| B、f(x-1)一定是偶函数 |
| C、f(x+1)一定是奇函数 |
| D、f(x+1)一定是偶函数 |
已知函数f(x)是定义在R上的偶函数,且在[0,+∞)上为增函数,若f(log2x)>f(1),则x的取值范围是( )
| A、(2,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1)∪(2,+∞) |
已知f(x)是定义在R上的奇函数,当x≥0时f(x)=ex+m(m为常数),则f(-ln5)的值为( )
| A、-4 | B、4 | C、-6 | D、6 |
函数f(x)=
+lg(x+1)的定义域为( )
| 3x2 | ||
|
| A、(-1,1) |
| B、(-1,+∞) |
| C、(1,+∞) |
| D、(-∞,1) |
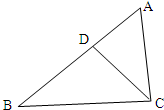 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=