题目内容
已知函数y=f(x)和y=g(x)在[-2,2]上的图象如图所示:给出下列四个命题:
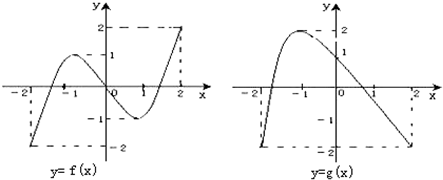
①方程f[g(x)]=0有且仅有6个根;
②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有7个根;
④方程g[g(x)]=0有且仅有4个根.
其中正确命题的序号为 .
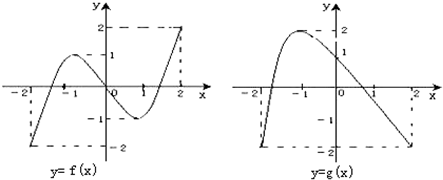
①方程f[g(x)]=0有且仅有6个根;
②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有7个根;
④方程g[g(x)]=0有且仅有4个根.
其中正确命题的序号为
考点:函数的图象
专题:函数的性质及应用
分析:把复合函数的定义域和值域进行对接,看满足外层函数为零时内层函数有几个自变量与之相对应.
解答:
解:①设t=g(x),则由f[g(x)]=0,即f(t)=0,则t1=0或-2<t2<-1或1<t3<2,
当t1=0时,t=g(x)有2个不同值,
当-2<t2<-1时,t=g(x)有2个不同值,
当1<t3<2,时,t=g(x)有2个不同值,∴方程f[g(x)]=0有且仅有6个根,故①正确.
②设t=f(x),若g[f(x)]=0,即g(t)=0,
则-2<t1<-1或0<t2<1,
当-2<t1<-1时,t=f(x)有1个不同值,
当0<t2<1时,t=f(x)有3个不同值,
∴方程g[f(x)]=0有且仅有4个根,故②错误.
③设t=f(x),若f[f(x)]=0,即f(t)=0,
则t1=0或-2<t2<-1或1<t3<2,
当t1=0时,t=f(x)有3个不同值,
当-2<t2<-1时,t=f(x)有1个不同值,
当1<t3<2,时,t=f(x)有1个不同值,∴方程f[f(x)]=0有且仅有5个根,故③错误.
④设t=g(x),若g[g(x)]=0,即g(t)=0,
则-2<t1<-1或0<t2<1,
当-2<t1<-1时,t=g(x)有2个不同值,
当0<t2<1时,t=g(x)有2个不同值,∴方程g[g(x)]=0有且仅有4个根,故④正确.
故正确的是①④,
故答案为:①④
当t1=0时,t=g(x)有2个不同值,
当-2<t2<-1时,t=g(x)有2个不同值,
当1<t3<2,时,t=g(x)有2个不同值,∴方程f[g(x)]=0有且仅有6个根,故①正确.
②设t=f(x),若g[f(x)]=0,即g(t)=0,
则-2<t1<-1或0<t2<1,
当-2<t1<-1时,t=f(x)有1个不同值,
当0<t2<1时,t=f(x)有3个不同值,
∴方程g[f(x)]=0有且仅有4个根,故②错误.
③设t=f(x),若f[f(x)]=0,即f(t)=0,
则t1=0或-2<t2<-1或1<t3<2,
当t1=0时,t=f(x)有3个不同值,
当-2<t2<-1时,t=f(x)有1个不同值,
当1<t3<2,时,t=f(x)有1个不同值,∴方程f[f(x)]=0有且仅有5个根,故③错误.
④设t=g(x),若g[g(x)]=0,即g(t)=0,
则-2<t1<-1或0<t2<1,
当-2<t1<-1时,t=g(x)有2个不同值,
当0<t2<1时,t=g(x)有2个不同值,∴方程g[g(x)]=0有且仅有4个根,故④正确.
故正确的是①④,
故答案为:①④
点评:本题考查根的存在性及根的个数判断,根据函数的图象,分别判断根的个数,考查学生的逻辑思维能力及识别图象的能力.

练习册系列答案
相关题目
当a,b∈R时,下列各式恒成立的是( )
A、(
| ||||||
B、(
| ||||||
C、
| ||||||
D、
|
已知数列{an}中满足a1=15,
=2,则
的最小值为( )
| an+1-an |
| n |
| an |
| n |
| A、10 | ||
B、2
| ||
| C、9 | ||
D、
|
正三棱柱ABC-A1B1C1中,各棱长均为2,M为AA1中点,N为BC的中点,则在棱柱的表面上从点M到点N的最短距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值,则( )
| A、f(x-1)一定是奇函数 |
| B、f(x-1)一定是偶函数 |
| C、f(x+1)一定是奇函数 |
| D、f(x+1)一定是偶函数 |
焦点为(0,6)且过点(2,5)双曲线方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|