Question

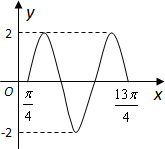在研究性学习中，我校高三某班的一个课题研究小组做“关于横波的研究实验”．根据实验记载，他们观察到某一时刻的波形曲线符合函数f（x）=2sin（ωx+φ）的图象，其部分图象如图所示，则f（0）=

 

．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由周期求出ω，由五点法作图求出φ的值，可得函数的解析式，从而求得f（0）的值．

解答： 解：由函数的图象可得

3

2

T=

3

2

•

2π

ω

=

13π

4

-

π

4

=3π，求得ω=1．
再根据五点法作图可得1×

π

4

+φ=0，∴φ=-

π

4

，∴f（x）=2sin（x-

π

4

），
故f（0）=2sin（-

π

4

）=-

2

，
故答案为：-

2

．

点评：本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，属于基础题．