题目内容
如果在约束条件
(0<a<1)下,目标函数x+ay最大值是
,则a=( )
|
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:简单线性规划的应用
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,令z=x+ay,化为y=-
x+
z,
z相当于直线y=-
x+
z的纵截距,则由目标函数x+ay最大值是
可得
+a
=
.
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 5 |
| 3 |
| 2 |
| a+1 |
| 2a |
| a+1 |
| 5 |
| 3 |
解答:
解:由题意作出其平面区域,

令z=x+ay,化为y=-
x+
z,
z相当于直线y=-
x+
z的纵截距,
由
解得,x=
,y=
,
则
+a
=
,
解得,a=
或
,
故选C.

令z=x+ay,化为y=-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
由
|
| 2 |
| a+1 |
| 2a |
| a+1 |
则
| 2 |
| a+1 |
| 2a |
| a+1 |
| 5 |
| 3 |
解得,a=
| 1 |
| 2 |
| 1 |
| 3 |
故选C.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
相关题目
已知数列{an}中满足a1=15,
=2,则
的最小值为( )
| an+1-an |
| n |
| an |
| n |
| A、10 | ||
B、2
| ||
| C、9 | ||
D、
|
已知f(x)=Asin(ωx+φ)(A>0,ω>0)在x=1处取最大值,则( )
| A、f(x-1)一定是奇函数 |
| B、f(x-1)一定是偶函数 |
| C、f(x+1)一定是奇函数 |
| D、f(x+1)一定是偶函数 |
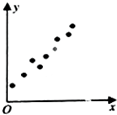 已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )
已知变量x与y呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
焦点为(0,6)且过点(2,5)双曲线方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
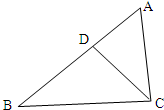 在△ABC中,∠A=60°,BC=
在△ABC中,∠A=60°,BC=