题目内容

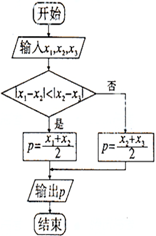
如图，当x1=6，x2=9，p=8.5时，x3等于（　　）
A、8B、4C、10D、9
考点：选择结构
专题：算法和程序框图
分析：执行程序框图，x1=6，x2=90，不满足条件|x1-x2|＜|x2-x1|，有p=
9+x3
2
=8.5，故可求得x3=8．
解答： 解：执行程序框图，有
x1=6，x2=90，
不满足条件|x1-x2|＜|x2-x1|，有p=
9+x3
2
，
由于p=8.5，故可求得x3=2×8.5-9=8．
故选：A．
点评：本题主要考察了程序框图和算法，属于基础题．
练习册系列答案
相关题目
已知：
a
=（
3
sinx，cosx），
b
=（cosx，cosx），f（x）=2
a
•
b
（x∈R）．
（1）求f（x）关于x的表达式，并求f（x）的最小正周期；
（2）已知g（x）=f（x）+2m-1，若x∈[0，
π
2
]时，g（x）的最小值为5，求m的值．
已知f（x）=Asin（ωx+φ）（A＞0，ω＞0）在x=1处取最大值，则（　　）
A、f（x-1）一定是奇函数
B、f（x-1）一定是偶函数
C、f（x+1）一定是奇函数
D、f（x+1）一定是偶函数
焦点为（0，6）且过点（2，5）双曲线方程是（　　）
A、
x2
20
-
y2
16
=1
B、
x2
16
-
y2
20
=1
C、
y2
20
-
x2
16
=1
D、
y2
16
-
x2
20
=1
过点P（2，1）的直线l与圆C：（x-1）2+y2=4交于A，B两点，当∠ACB最小时，直线l的方程为
 
．
若x，y满足不等式组 
x-y≥0
2x-y-10≤0
3
x+y-5
3
≥0
，则2x+y的最大值是
 
．
已知a＞0且a≠1，f（x）=x2，g（x）=ax+
1
4
，当x∈（-1，1）时f（x）＜g（x）恒成立，则实数a的取值范围
 
．
等差数列{an}中a3×a7=-16，a4+a6=0，则前项n和Sn=
 
．
已知f（x）是定义在R上的奇函数，当x≥0时f（x）=ex+m（m为常数），则f（-ln5）的值为（　　）
A、-4B、4C、-6D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网