题目内容

在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c，且满足（b-c-a）（b-c+a）+bc=0．
（1）求∠A的大小；
（2）若f（x）=
3
sin
x
2
cos
x
2
+cos2
x
2
，求f（B）的取值范围．
考点：余弦定理,三角函数中的恒等变换应用
专题：解三角形
分析：（1）利用余弦定理表示出cosA，将已知等式整理后代入计算求出cosA的值，即可确定出A的度数；
（2）f（x）解析式利用二倍角的正弦、余弦函数公式化简，再利用两角和与差的正弦函数公式化为一个角的正弦函数，利用正弦函数的值域即可确定出f（B）的范围．
解答： 解：（1）∵在锐角△ABC中，（b-c-a）（b-c+a）+bc=（b-c）2-a2+bc=b2+c2-a2-bc=0，即b2+c2-a2=bc，
∴cosA=
b2+c2-a2
2bc
=
bc
2bc
=
1
2
，
∴A=60°；
（2）f（B）=
3
2
sinB+
1
2
（cosB+1）=
3
2
sinB+
1
2
cosB+
1
2
=sin（B+30°）+
1
2
，
∵锐角△ABC，0＜B＜90°，
∴30°＜B+30°＜120°，即
1
2
＜sin（B+30°）＜1，
则f（B）的取值范围为（1，
3
2
）．
点评：此题考查了余弦定理，以及三角函数中的恒等变换应用，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
若抛物线x2=2py（p＞0）的焦点与双曲线
y2
3
-x2=1的一个焦点重合，则p的值为（　　）
A、-2B、2C、-4D、4
已知函数f（x）的定义域为R，当x＞0时，f（x）＞1，且对任意实数x，y恒有f（x+y）=f（x）+f（y）-1．
（1）试探究函数f（x）的单调性．
（2）若f（2）=3，试解不等式f（x2）+f（1-4x）＜6．
已知向量
a
=（2+cos（2x-
π
3
），sinx-cosx），
b
=（1，sinx+cosx），函数f（x）=
a
•
b
-m（x∈R）在区间[-
π
24
，
5π
12
]上的最小值为-
2
2
．
（Ⅰ）求实数m的值；
（Ⅱ）在△ABC中，角A，B，C所对的边是a，b，c．若A为锐角，且满足f（A）=1，sinB=2sinC，△ABC面积为
3
，求边长a．
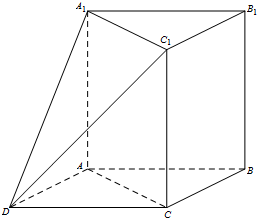如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1． 
（Ⅰ）求证：A1D∥平面BCC1B1；
（Ⅱ）求证：AC⊥平面ADA1．
已知x≠0，函数f（x）满足f（x+
1
x
）=2x2+
2
x2
-1，求f（5）的值．
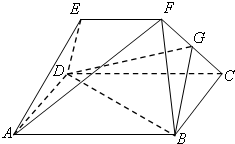如图几何体中，四边形ABCD为矩形，AB=2BC=4，BF=CF=AE=DE，EF=2，EF∥AB，AF⊥CF．
（Ⅰ）若G为FC的中点，证明：AF∥面BDG；
（Ⅱ）求二面角A-BF-C的余弦值．
某产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：
 x  2  4  5  6  8
 y  30  40  60  50  70
（1）画出上表数据的散点图；
（2）根据上表提供的数据，求出y关于x的线性回归方程；
（3）据此估计广告费用为10万元时，所得的销售收入．
（参考数值：
5
i=1
x
2
i
=145，
5
i=1
xiyi=1380，参考公式：b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
=
n
i=1
xiyi-
.
x
.
y
n
i=1
x
2
i
-n
.
x2
，a=
.
y
-b
.
x
）
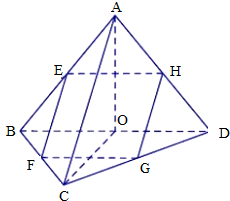在三棱锥A-BCD中，点E、F、G、H分别是AB、BC、CD、DA的中点．
（Ⅰ）若AC=BD，求证：四边形EFGH为菱形；
（Ⅱ）若AB=AD，BC=CD，且O为BD中点，求证：BD⊥平面AOC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网