题目内容
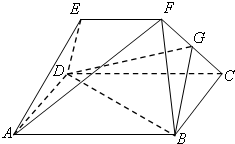 如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.
如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.(Ⅰ)若G为FC的中点,证明:AF∥面BDG;
(Ⅱ)求二面角A-BF-C的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)连接AC交BD于O点,利用三角形中位线定理得到OG∥AF,由此能证明AF∥面BDG.
(Ⅱ)以P为原点,PF为z轴建立空间直角坐标系,利用向量法能求出二面角A-BF-C的余弦值.
(Ⅱ)以P为原点,PF为z轴建立空间直角坐标系,利用向量法能求出二面角A-BF-C的余弦值.
解答:
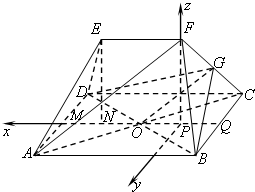 (Ⅰ)证明:连接AC交BD于O点,则O为AC的中点,
(Ⅰ)证明:连接AC交BD于O点,则O为AC的中点,
连接OG,因为点G为FC中点,所以OG为△AFC的中位线,
所以OG∥AF…(2分)
∵AF?面BDG,OG?面BDG,
所以AF∥面BDG.…(4分)
(Ⅱ)解:取AD中点M,BC的中点Q,连接MQ,
则MQ∥AB∥EF,所以MQFE共面,
作FP⊥MQ于P,EN⊥MQ于N,则EN∥FP且EN=FP,
∵AE=DE=BF=CF,AD=BC,∴△ADE和△BCF全等,
∴EM=FQ,∴△ENM和△FPQ全等,
∴MN=PQ=1∵BF=CF,Q为BC中点,∴BC⊥FQ,
又BC⊥MQ,FQ∩MQ=Q,∴BC⊥面MQFE,
∴PF⊥BC,∴PF⊥面ABCD,…(6分)
以P为原点,PF为z轴建立空间直角坐标系如图所示,
则A(3,1,0),B(-1,1,0),C(-1,-1,0),
设F(0,0,h),则
=(-3,-1,h),
=(1,1,h),
∵AF⊥CF,∴
•
=0⇒-3-1+h2=0⇒h=2
设面ABF的法向量
=(x1,y1,z1),
∵
=(-3,-1,2),
=(1,-1,2)
∴由
⇒
,
令z1=1,得
=(0,2,1)…(8分)
设面CBF的法向量
=(x2,y2,z2),
∵
=(1,-1,2),
=(0,-2,0),
∴由
⇒
,
令z2=1,得
=(-2,0,1)…(10分)
∴cos<
,
>=
=
=
设二面角A-BF-C的平面角为θ,
则cosθ=cos(π-<
,
>)=-cos<
,
>=-
.…(12分)
 (Ⅰ)证明:连接AC交BD于O点,则O为AC的中点,
(Ⅰ)证明:连接AC交BD于O点,则O为AC的中点,连接OG,因为点G为FC中点,所以OG为△AFC的中位线,
所以OG∥AF…(2分)
∵AF?面BDG,OG?面BDG,
所以AF∥面BDG.…(4分)
(Ⅱ)解:取AD中点M,BC的中点Q,连接MQ,
则MQ∥AB∥EF,所以MQFE共面,
作FP⊥MQ于P,EN⊥MQ于N,则EN∥FP且EN=FP,
∵AE=DE=BF=CF,AD=BC,∴△ADE和△BCF全等,
∴EM=FQ,∴△ENM和△FPQ全等,
∴MN=PQ=1∵BF=CF,Q为BC中点,∴BC⊥FQ,
又BC⊥MQ,FQ∩MQ=Q,∴BC⊥面MQFE,
∴PF⊥BC,∴PF⊥面ABCD,…(6分)
以P为原点,PF为z轴建立空间直角坐标系如图所示,
则A(3,1,0),B(-1,1,0),C(-1,-1,0),
设F(0,0,h),则
| AF |
| CF |
∵AF⊥CF,∴
| AF |
| CF |
设面ABF的法向量
| n1 |
∵
| AF |
| BF |
∴由
|
|
令z1=1,得
| n1 |
设面CBF的法向量
| n2 |
∵
| BF |
| BC |
∴由
|
|
令z2=1,得
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 5 |
设二面角A-BF-C的平面角为θ,
则cosθ=cos(π-<
| n1 |
| n2 |
| n1 |
| n2 |
| 1 |
| 5 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
复数z=i2(i是虚数单位)的虚部是( )
| A、i | B、-1 | C、1 | D、0 |
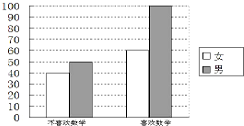 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图. 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC. 某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).
某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).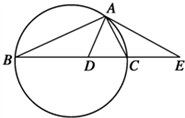 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与