题目内容
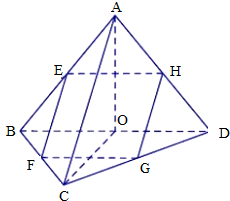 在三棱锥A-BCD中,点E、F、G、H分别是AB、BC、CD、DA的中点.
在三棱锥A-BCD中,点E、F、G、H分别是AB、BC、CD、DA的中点.(Ⅰ)若AC=BD,求证:四边形EFGH为菱形;
(Ⅱ)若AB=AD,BC=CD,且O为BD中点,求证:BD⊥平面AOC.
考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)利用三角形中位线定理能证明四边形EFGH为菱形.
(Ⅱ)利用等腰三角形性质和直线与平面垂直的判定定理能证明BD⊥平面AOC.
(Ⅱ)利用等腰三角形性质和直线与平面垂直的判定定理能证明BD⊥平面AOC.
解答:
(Ⅰ)证明:∵点E、F、G、H分别是AB、BC、CD、DA的中点,
∴EH
BD,FG
BD,EF
AC,HG
AC,
∵AC=BD,∴四边形EFGH为菱形.
(Ⅱ)证明:∵AB=AD,BC=CD,且O为BD中点,
∴AO⊥BD,CO⊥BD,
∵CO∩AO=O,
∴BD⊥平面AOC.
∴EH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∵AC=BD,∴四边形EFGH为菱形.
(Ⅱ)证明:∵AB=AD,BC=CD,且O为BD中点,
∴AO⊥BD,CO⊥BD,
∵CO∩AO=O,
∴BD⊥平面AOC.
点评:本题考查四边形为菱形的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
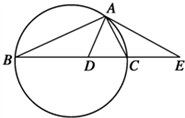 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与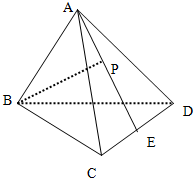 已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.
已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.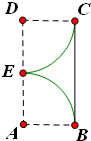 如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为
如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为