题目内容
已知函数f(x)的定义域为R,当x>0时,f(x)>1,且对任意实数x,y恒有f(x+y)=f(x)+f(y)-1.
(1)试探究函数f(x)的单调性.
(2)若f(2)=3,试解不等式f(x2)+f(1-4x)<6.
(1)试探究函数f(x)的单调性.
(2)若f(2)=3,试解不等式f(x2)+f(1-4x)<6.
考点:抽象函数及其应用,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)令x=y=0,求出f(0)=1,令y=-x得到f(x)+f(-x)=2,令x1<x2,由条件推出f(x1)<f(x2),即可判断f(x)的单调性;
(2)运用赋值,求出f(4)=5,由条件,得到f[x2+(1-4x)]<f(4),再由单调性,得到x2+(1-4x)<4
求出解集即可.
(2)运用赋值,求出f(4)=5,由条件,得到f[x2+(1-4x)]<f(4),再由单调性,得到x2+(1-4x)<4
求出解集即可.
解答:
解:(1)令x=y=0则f(0)=2f(0)-1,f(0)=1,
令y=-x,则f(0)=f(x)+f(-x)-1=1,f(x)+f(-x)=2
令x1<x2,则x2-x1>0,
∵x>0时f(x)>1
∴f(x2-x1)>1
即f(x2)+f(-x1)-1>1
∵f(-x1)+f(x1)=2
∴f(x2)-f(x1)>0即f(x1)<f(x2)
∴f(x)在R上是增函数;
(2)∵f(2)=3,
∴f(4)=2f(2)-1=2×3-1=5
又f(x2)+f(1-4x)<6即1+f[x2+(1-4x)]<6
f[x2+(1-4x)]<5=f(4)
∵f(x)在R上是增,
∴x2+(1-4x)<4
∴2-
<x<2+
即解集为(2-
,2+
).
令y=-x,则f(0)=f(x)+f(-x)-1=1,f(x)+f(-x)=2
令x1<x2,则x2-x1>0,
∵x>0时f(x)>1
∴f(x2-x1)>1
即f(x2)+f(-x1)-1>1
∵f(-x1)+f(x1)=2
∴f(x2)-f(x1)>0即f(x1)<f(x2)
∴f(x)在R上是增函数;
(2)∵f(2)=3,
∴f(4)=2f(2)-1=2×3-1=5
又f(x2)+f(1-4x)<6即1+f[x2+(1-4x)]<6
f[x2+(1-4x)]<5=f(4)
∵f(x)在R上是增,
∴x2+(1-4x)<4
∴2-
| 7 |
| 7 |
即解集为(2-
| 7 |
| 7 |
点评:本题主要考查函数的单调性及应用,注意定义的运用,同时考查解决抽象函数的常用方法:赋值法,务必掌握.

练习册系列答案
相关题目
在极坐标系中与圆ρ=4sin(θ+
)相切的一条直线的方程为( )
| π |
| 4 |
A、ρsin(θ-
| ||
| B、ρsinθ=4 | ||
| C、ρcosθ=4 | ||
D、ρcos(θ-
|
复数z=i2(i是虚数单位)的虚部是( )
| A、i | B、-1 | C、1 | D、0 |
下列各式中值为
的是( )
| ||
| 2 |
| A、sin45°cos15°+cos45°sin15° | ||
| B、sin45°cos15°-cos45°sin15° | ||
| C、cos75°cos30°+sin75°sin30° | ||
D、
|
若存在x∈[-2,3],使不等式2x-x2≥a成立,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-8] |
| C、[1,+∞) |
| D、[-8,+∞) |
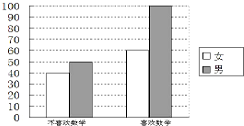 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.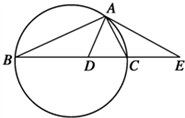 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与