题目内容
某产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
(1)画出上表数据的散点图;
(2)根据上表提供的数据,求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.
(参考数值:
=145,
xiyi=1380,参考公式:b=
=
,a=
-b
)
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)根据上表提供的数据,求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.
(参考数值:
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| |||||||
|
| |||||||
|
. |
| y |
. |
| x |
考点:线性回归方程
专题:应用题,概率与统计
分析:(1)根据表中所给的五对数据,得到五个有序数对,在平面直角坐标系中画出点,得到散点图.
(2)先做出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法做出线性回归方程的系数,再做出a的值,求出线性回归方程.
(3)把所给的x的值代入线性回归方程,求出y的值,这里的y的值是一个预报值,或者说是一个估计值.
(2)先做出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法做出线性回归方程的系数,再做出a的值,求出线性回归方程.
(3)把所给的x的值代入线性回归方程,求出y的值,这里的y的值是一个预报值,或者说是一个估计值.
解答:
解:(1)根据表中所列数据可得散点图如下:
 …(3分)
…(3分)
(2)求回归直线方程;
=
=5,
=
=50…(4分)b=
=
=6.5…(6分)
∴a=
-b
=50-6.5×5=17.5…(8分)
因此,所求回归直线方程为:
=6.5x+17.5.…(9分)
(3)根据上面求得的回归直线方程,
当广告费支出为10万元时,
=6.5×10+17.5=82.5万元
即这种产品的销售收入大约为82.5万元.…(12分)
 …(3分)
…(3分)(2)求回归直线方程;
. |
| x |
| 2+4+5+6+8 |
| 5 |
. |
| y |
| 30+40+60+50+70 |
| 5 |
| |||||||
|
| 1380-5×5×50 |
| 145-5×5×5 |
∴a=
. |
| y |
. |
| x |
因此,所求回归直线方程为:
 |
| y |
(3)根据上面求得的回归直线方程,
当广告费支出为10万元时,
 |
| y |
即这种产品的销售收入大约为82.5万元.…(12分)
点评:本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法求出线性回归方程的系数,考查学生的运算能力.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
下列各式中值为
的是( )
| ||
| 2 |
| A、sin45°cos15°+cos45°sin15° | ||
| B、sin45°cos15°-cos45°sin15° | ||
| C、cos75°cos30°+sin75°sin30° | ||
D、
|
 某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).
某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).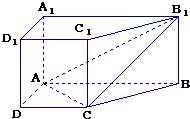 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.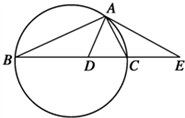 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与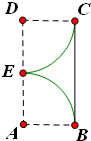 如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为
如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为