题目内容
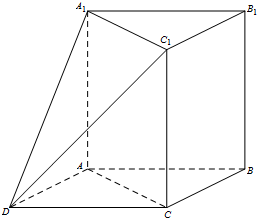 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. (Ⅰ)求证:A1D∥平面BCC1B1;
(Ⅱ)求证:AC⊥平面ADA1.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)线面平行的判定定理即可证明;
(Ⅱ)线面垂直的判定定理即可证明.
(Ⅱ)线面垂直的判定定理即可证明.
解答:
 (本小题共13分)
(本小题共13分)
证明:
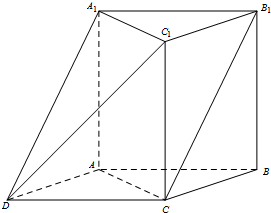
(Ⅰ)连结B1C,∵三棱柱ABC-A1B1C1中A1B1∥AB且A1B1=AB,
由ABCD为平行四边形得CD∥AB且CD=AB
∴A1B1∥CD且A1B1=CD------------------(2分)
∴四边形A1B1CD为平行四边形,A1D∥B1C---------(4分)
∵B1C?平面BCC1B1,A1D?平面BCC1B1-----------(6分)
∴A1D∥平面BCC1B1------------------(7分)
(Ⅱ)∵平行四边形ABCD中,AC⊥BC,
∴AC⊥AD------------------(2分)
∵AA1⊥平面ABC,AC?平面ABC
∴AA1⊥AC------------------(4分)
又∵AD∩AA1=A,AA1?平面ADA1,AD?平面ADA1,
∴AC⊥平面ADA1.------------------(6分)
 (本小题共13分)
(本小题共13分)证明:
(Ⅰ)连结B1C,∵三棱柱ABC-A1B1C1中A1B1∥AB且A1B1=AB,
由ABCD为平行四边形得CD∥AB且CD=AB
∴A1B1∥CD且A1B1=CD------------------(2分)
∴四边形A1B1CD为平行四边形,A1D∥B1C---------(4分)
∵B1C?平面BCC1B1,A1D?平面BCC1B1-----------(6分)
∴A1D∥平面BCC1B1------------------(7分)
(Ⅱ)∵平行四边形ABCD中,AC⊥BC,
∴AC⊥AD------------------(2分)
∵AA1⊥平面ABC,AC?平面ABC
∴AA1⊥AC------------------(4分)
又∵AD∩AA1=A,AA1?平面ADA1,AD?平面ADA1,
∴AC⊥平面ADA1.------------------(6分)
点评:本题考查线面平行与线面垂直的判定.

练习册系列答案
相关题目
命题“若α=
,则tanα=
”的逆否命题是( )
| π |
| 3 |
| 3 |
A、若α≠
| ||||
B、若α=
| ||||
C、若tanα≠
| ||||
D、若tanα=
|
若存在x∈[-2,3],使不等式2x-x2≥a成立,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-8] |
| C、[1,+∞) |
| D、[-8,+∞) |
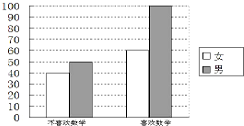 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图. 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.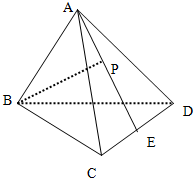 已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.
已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.