题目内容
已知向量
=(2+cos(2x-
),sinx-cosx),
=(1,sinx+cosx),函数f(x)=
•
-m(x∈R)在区间[-
,
]上的最小值为-
.
(Ⅰ)求实数m的值;
(Ⅱ)在△ABC中,角A,B,C所对的边是a,b,c.若A为锐角,且满足f(A)=1,sinB=2sinC,△ABC面积为
,求边长a.
| a |
| π |
| 3 |
| b |
| a |
| b |
| π |
| 24 |
| 5π |
| 12 |
| ||
| 2 |
(Ⅰ)求实数m的值;
(Ⅱ)在△ABC中,角A,B,C所对的边是a,b,c.若A为锐角,且满足f(A)=1,sinB=2sinC,△ABC面积为
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,正弦定理
专题:三角函数的图像与性质
分析:(Ⅰ)根据向量的数量积求得函数解析式,并利用两角和公式和二倍角公式化简,根据x的范围和正弦函数的单调性求得函数的最小值表达式进而求得m.
(Ⅱ)先根据f(A)=1求得A,进而根据正弦定理判断出b=2c,进而利用三角形面积求得bc的值,联立方程分别求得b和c,最后利用余弦定理求得a的值.
(Ⅱ)先根据f(A)=1求得A,进而根据正弦定理判断出b=2c,进而利用三角形面积求得bc的值,联立方程分别求得b和c,最后利用余弦定理求得a的值.
解答:
解:(Ⅰ)f(x)=
•
-m=2+cos(2x-
)+(sinx-cosx)(sinx+cosx)-m
=cos2xcos
+sin2xsin
-cos2x+2-m
=
sin2x-
cos2x+2-m
=sin(2x-
)+2-m,
因为x∈[-
,
],
则-
≤2x-
≤
,
函数f(x)在2x-
=-
时取得最小值-
+2-m=-
,解得m=2.
(Ⅱ)由f(A)=1且A为锐角解得A=
,
又因为sinB=2sinC,由正弦定理得b=2c,
又因为△ABC的面积为
,所以S△ABC=
bcsinA=
即bc=4,
由①②解得b=2
,c=
,
又由余弦定理a2=b2+c2-2bccosA可得a=
.
| a |
| b |
| π |
| 3 |
=cos2xcos
| π |
| 3 |
| π |
| 3 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
因为x∈[-
| π |
| 24 |
| 5π |
| 12 |
则-
| π |
| 4 |
| π |
| 6 |
| 2π |
| 3 |
函数f(x)在2x-
| π |
| 6 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)由f(A)=1且A为锐角解得A=
| π |
| 3 |
又因为sinB=2sinC,由正弦定理得b=2c,
又因为△ABC的面积为
| 3 |
| 1 |
| 2 |
| 3 |
由①②解得b=2
| 2 |
| 2 |
又由余弦定理a2=b2+c2-2bccosA可得a=
| 6 |
点评:本题主要考查了三角函数恒等变换的应用,正弦定理和余弦定理的应用.综合考查了学生运用三角函数知识分析和解决问题的能力.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
下列各式中值为
的是( )
| ||
| 2 |
| A、sin45°cos15°+cos45°sin15° | ||
| B、sin45°cos15°-cos45°sin15° | ||
| C、cos75°cos30°+sin75°sin30° | ||
D、
|
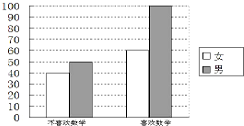 为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.
为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图. 某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).
某市为了配合宣传新《道路交通法》举办有奖征答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示.(如图是样本频率分布直方图,表是对样本中回答正确人数的分析统计表).