题目内容
已知x≠0，函数f（x）满足f（x+
）=2x2+
-1，求f（5）的值．
| 1 |
| x |
| 2 |
| x2 |
考点：函数解析式的求解及常用方法
专题：计算题,函数的性质及应用
分析：先利用配凑法求出f（x），代入x=5即可求得．
解答：
解：f（x+
）=2x2+
-1=2(x+
)2-5，
∴f（x）=2x2-5，f（5）=2×52-5=45．
| 1 |
| x |
| 2 |
| x2 |
| 1 |
| x |
∴f（x）=2x2-5，f（5）=2×52-5=45．
点评：该题考查函数解析式的求解，属基础题，熟练掌握常见函数解析式的求法是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
等差数列{an}的前项n和为Sn，满足S35=S3992，
=（1，an），
=（2014，a2014），则
•
的值为（ ）
| a |
| b |
| a |
| b |
| A、2014 | B、-2014 |
| C、1 | D、0 |
某市为了配合宣传新《道路交通法》举办有奖征答活动，随机对该市15～65岁的人群抽样了n人，回答问题统计结果如图表所示．（如图是样本频率分布直方图，表是对样本中回答正确人数的分析统计表）．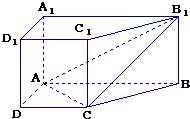
直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．