Question

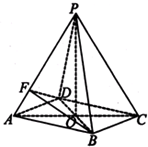如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，PB=PD=

6

，AP=4AF．
（1）求证：PO⊥底面ABCD；
（2）求多面体PBCDF的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定

专题：综合题,空间位置关系与距离

分析：（1）证明PO⊥底面ABCD，只需证明PO⊥AC，PO⊥BD；
（2）求出四棱锥P-ABCD的体积、三棱锥F-ABD的体积，即可求出多面体PBCDF的体积．

解答： （1）证明：因为底面ABCD是菱形，AC∩BD=O，
所以O为AC，BD中点．-------------------------------------（1分）
又因为PA=PC，PB=PD，
所以PO⊥AC，PO⊥BD，---------------------------------------（3分）
所以PO⊥底面ABCD．…（5分）
（2）解：由△AB

F

1

是边长为2的等边三角形知AC=2，PO=

3

又PB=PD=

6

，所以BO=DO=

3

，BD=2

3

因四边形ABCD为菱形，所以其面积为

1

2

AC×BD=

1

2

×2×2

3

=2

3

由（1）知四棱锥P-ABCD的体积为

1

3

×2

3

×

3

=2．…（8分）
在AO上取点G，使AG=

1

4

AO，连FG，则FG∥PO
由（1）可知FG⊥平面ABCD
于是三棱锥F-ABD的体积为

1

3

×S△ABD×FG=

1

3

×

3

×

1

4

×

3

=

1

4

故多面体PBCDF的体积为2-

1

4

=

7

4

．…（12分）

点评：本题考查线面垂直，考查了用分割法求多面体的体积，考查了学生的空间想象能力与推理论证能力．