题目内容
在直角坐标系xOy中,圆C的参数方程为
(θ为参数),直线l经过点P(3,2),且倾斜角为
.
(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A、B两点,求|PA|•|PB|的值.
|
| π |
| 3 |
(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A、B两点,求|PA|•|PB|的值.
考点:圆的参数方程
专题:坐标系和参数方程
分析:(Ⅰ)把圆C的参数方程消去参数,化为直角坐标方程,由条件求得直线l的参数方程.
(Ⅱ)把直线l的参数方程代入圆C的方程化简可得 t2+(3+2
)t-12=0,利用韦达定理求得 t1•t2的值,从而求得|PA|•|PB|=|t1•t2|的值.
(Ⅱ)把直线l的参数方程代入圆C的方程化简可得 t2+(3+2
| 3 |
解答:
解:(Ⅰ)把圆C的参数方程为
(θ为参数),消去参数,化为直角坐标方程为 x2+y2=25,
由条件可得 直线l的参数方程为
,即
(t为参数).
(Ⅱ)把直线l的参数方程代入圆C的方程化简可得 t2+(3+2
)t-12=0,
利用韦达定理可得 t1•t2=-12,故|PA|•|PB|=|t1•t2|=12.
|
由条件可得 直线l的参数方程为
|
|
(Ⅱ)把直线l的参数方程代入圆C的方程化简可得 t2+(3+2
| 3 |
利用韦达定理可得 t1•t2=-12,故|PA|•|PB|=|t1•t2|=12.
点评:本题主要考查把参数方程为直角坐标方程的方法,韦达定理的应用,参数的几何意义,属于基础题.

练习册系列答案
相关题目
一个圆柱的母线长度为2,底为半径为1的圆,则此圆柱的侧面积是( )
| A、π | B、2π | C、3π | D、4π |
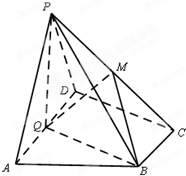 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=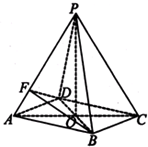 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=