题目内容

圆x2+y2-2x+2y=0的圆心坐标为（　　）
A、（1，-1）
B、（1，0）
C、（-1，-1）
D、（1，1）
考点：圆的一般方程
专题：直线与圆
分析：圆x2+y2+Dx+Ey+F=0的圆心（-
D
2
，-
E
2
），由此能求出结果．
解答： 解：∵圆x2+y2+Dx+Ey+F=0的圆心（-
D
2
，-
E
2
），
∴圆x2+y2-2x+2y=0的圆心坐标为：（1，-1）．
故选：A．
点评：本题考查圆的坐标的求法，是基础题，解题时要认真审题，注意圆的一般方程的性质的灵活运用．
练习册系列答案
相关题目
观察下列各式：
2-
2
5
=2
2
5
，
3-
3
10
=3
3
10
，
4-
4
17
=4
4
17
，…．若
9-
m
n
=9
m
n
，则n-m=（　　）
A、43B、57C、73D、91
若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1的值为（　　）
A、1B、129
C、128D、127
等差数列{an}中，若a7-a3=20，则a2014-a2008=（　　）
A、40B、30C、25D、20
一个圆柱的母线长度为2，底为半径为1的圆，则此圆柱的侧面积是（　　）
A、πB、2πC、3πD、4π
点（1，0）到直线3x+4y-8=0的距离为（　　）
A、1B、2C、3D、4
已知等比数列{an}的前n项和Sn=2n+m（m∈R）．
（1）求m的值及{an}的通项公式；
（2）设bn=2log2an-13，数列{bn}的前n项和为Tn，求Tn的最小值．
如图，四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，AA1=AB=2，E为棱AA1的中点．
（Ⅰ）求证：B1C1⊥CE；
（Ⅱ）求二面角B1-CE-C1的正弦值．
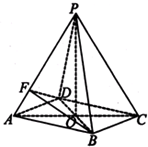如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，PB=PD=
6
，AP=4AF．
（1）求证：PO⊥底面ABCD；
（2）求多面体PBCDF的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网