题目内容
某小学四年级男同学有45名,女同学有30名,老师按照分层抽样的方法组建了一个5人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(Ⅰ)某同学被抽到的概率为样本容量除以个体总数,设有x名男同学被抽到,则由
=
,求得x的值,可得样本中男、女同学的人数.
(Ⅱ)把3名男同学和2名女同学分别记为a,b,c,m,n,用列举法求出所有的基本事件个数,再求得抽取的两名同学中恰有一名女同学的基本事件的个数,从而求得抽取的两名同学中恰有一名女同学的概率.
| 45 |
| x |
| 75 |
| 5 |
(Ⅱ)把3名男同学和2名女同学分别记为a,b,c,m,n,用列举法求出所有的基本事件个数,再求得抽取的两名同学中恰有一名女同学的基本事件的个数,从而求得抽取的两名同学中恰有一名女同学的概率.
解答:
解:(Ⅰ)某同学被抽到的概率为P=
=
,
设有x名男同学被抽到,则有
=
,∴x=3,
∴抽到的男同学为3人,女同学为2人.
(Ⅱ)把3名男同学和2名女同学分别记为a,b,c,m,n,则选取2名同学的基本事件有:
(a,b,),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),
(c,n),(m,n),(b,a),(c,a),(m,a),(n,a),(c,b),(m,b),
(n,b),(m,c),(n,c),(n,m),共20个,
基中恰好有一名女同学有(a,m),(a,n),(b,m),(b,n)(c,m),(c,n),
(m,a),(n,a),(m,b),(n,b),(m,c),(n,c),共计12 个,
选出的两名同学中恰有一名女同学的概率为
=
.
| 5 |
| 45+30 |
| 1 |
| 15 |
设有x名男同学被抽到,则有
| 45 |
| x |
| 75 |
| 5 |
∴抽到的男同学为3人,女同学为2人.
(Ⅱ)把3名男同学和2名女同学分别记为a,b,c,m,n,则选取2名同学的基本事件有:
(a,b,),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),
(c,n),(m,n),(b,a),(c,a),(m,a),(n,a),(c,b),(m,b),
(n,b),(m,c),(n,c),(n,m),共20个,
基中恰好有一名女同学有(a,m),(a,n),(b,m),(b,n)(c,m),(c,n),
(m,a),(n,a),(m,b),(n,b),(m,c),(n,c),共计12 个,
选出的两名同学中恰有一名女同学的概率为
| 12 |
| 20 |
| 3 |
| 5 |
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.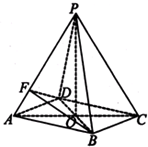 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=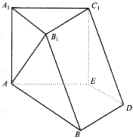 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2. 某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.
某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.