题目内容
六张卡片上分别写有数字1,2,3,3,4,5,从中任取四张排成一排,可以组成不同的四位偶数的个数为 .
考点:计数原理的应用
专题:排列组合
分析:根据分类计数原理,两个3中,可以选一个,不选,选2个三种情况,分类后再排末尾,问题得以解决.
解答:
解:第一类,不3选时,有
•
=12种,
第二类,选一个3时,有
•
•
=36种,
第三类,同时选两个3时,有
•
•
×
=18种,
根据分类计数原理得12+36+18=66种.
故答案为:66.
| A | 1 2 |
| A | 3 3 |
第二类,选一个3时,有
| C | 2 3 |
| A | 3 3 |
| A | 1 2 |
第三类,同时选两个3时,有
| C | 1 3 |
| A | 3 3 |
| A | 1 2 |
| 1 |
| 2 |
根据分类计数原理得12+36+18=66种.
故答案为:66.
点评:本题考查了分类计数原理,注意特殊元素的分类问题,属于中档题.

练习册系列答案
相关题目
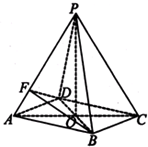 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=