题目内容
2013年6月“神州十号”发射成功,全国瞩目,这次发射过程共有三个值得关注的环节,即发射、授课、返回.据统计,由于时间关系,某班同学收看这三个环节的直播的概率分别为
,
,
,并且各个环节直播收看互不影响.
(1)若从该班随机选取4名同学,求这4名同学至少有2名同学收看了发射直播又收看了返回直播的概率;
(2)若用ε表示一位同学收看环节数,求ε的分布列与期望值.
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
(1)若从该班随机选取4名同学,求这4名同学至少有2名同学收看了发射直播又收看了返回直播的概率;
(2)若用ε表示一位同学收看环节数,求ε的分布列与期望值.
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:概率与统计
分析:(1)一名同学既收看了发射直播又收看了返回直播的概率为p=
×
=
,由此能求出这4名同学至少有2名同学收看了发射直播又收看了返回直播的概率.
(2)由条件知ε的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ε的分布列与期望值.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(2)由条件知ε的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ε的分布列与期望值.
解答:
解:(1)设“这4名同学至少有2名同学收看了发射直播又收看了返回直播”为事件A,
一名同学既收看了发射直播又收看了返回直播的概率为:
p=
×
=
,
∴P(A)=
(
)2(1-
)2+
(
)3(1-
)+(
)4=
.
(2)由条件知ε的可能取值为0,1,2,3,
P(ε=0)=(1-
)(1-
)(1-
)=
,
P(ε=1)=
×(1-
)×(1-
)+(1-
)×
×(1-
)+(1-
)×(1-
)×
=
,
P(ε=2)=
×
×(1-
)+
×(1-
)×
+(1-
)×
×
=
,
P(ε=3)=
×
×
=
,
∴ε的分布列为:
E?=0×
+1×
+2×
+3×
=
.
一名同学既收看了发射直播又收看了返回直播的概率为:
p=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴P(A)=
| C | 2 4 |
| 1 |
| 6 |
| 1 |
| 6 |
| C | 3 4 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 19 |
| 144 |
(2)由条件知ε的可能取值为0,1,2,3,
P(ε=0)=(1-
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 15 |
P(ε=1)=
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 11 |
| 30 |
P(ε=2)=
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 13 |
| 30 |
P(ε=3)=
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 15 |
∴ε的分布列为:
| ? | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 15 |
| 11 |
| 30 |
| 13 |
| 30 |
| 2 |
| 15 |
| 49 |
| 30 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题.

练习册系列答案
相关题目
点(1,0)到直线3x+4y-8=0的距离为( )
| A、1 | B、2 | C、3 | D、4 |
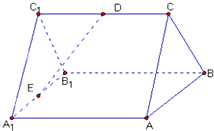 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.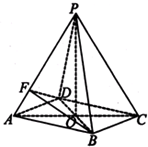 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=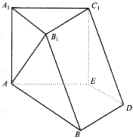 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2. 某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.
某校高三年段共有1000名学生,将其按专业发展取向分成普理、普文、艺体三类,如图是这三类的人数比例示意图.为开展某项调查,采用分层抽样的方法从这1000名学生中抽取一个容量为10的样本.