题目内容
已知函数f(x)=-3x2+3,定义数列{an}满足a1=3,且an>0,an+1=
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
,数列{bn}的前n项和为Sn,求证:Sn<
.
| -3f(an)+9 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
| 1 |
| an |
| 1 |
| 2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件得an+1=
=3an,由此能求出an=3n.
(Ⅱ)由bn=
=
,利用等比数列前n项和公式能证明Sn=
[1-(
)n]<
.
| -3(-3an2+3)+9 |
(Ⅱ)由bn=
| 1 |
| an |
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
(Ⅰ)解:∵f(x)=-3x2+3,数列{an}满足a1=3,
且an>0,an+1=
,
∴an+1=
=3an,
∴{an}是首项为3,公比为3的等比数列,
∴an=3n.
(Ⅱ)证明:∵bn=
=
,
∴Sn=
+
+…+
=
=
[1-(
)n],
∴Sn=
[1-(
)n]<
.
且an>0,an+1=
| -3f(an)+9 |
∴an+1=
| -3(-3an2+3)+9 |
∴{an}是首项为3,公比为3的等比数列,
∴an=3n.
(Ⅱ)证明:∵bn=
| 1 |
| an |
| 1 |
| 3n |
∴Sn=
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
=
| ||||
1-
|
=
| 1 |
| 2 |
| 1 |
| 3 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查数列的通项公式的证明,考查不等式的证明,解题时要注意等比数列的性质的灵活运用.

练习册系列答案
相关题目
等差数列{an}中,若a7-a3=20,则a2014-a2008=( )
| A、40 | B、30 | C、25 | D、20 |
 如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.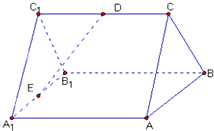 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点,E为底面一边A1B1的中点.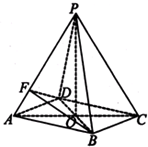 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=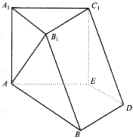 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.