题目内容
已知递增等差数列{an}中的a2,a5是函数f(x)=x2-7x+10的两个零点.数列{bn}满足,点(bn,Sn)在直线y=-x+1上,其中Sn是数列{bn}的前n项和.
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an•bn,求数列{cn}的前n项和Tn.
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an•bn,求数列{cn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)先解出两个零点,再利用等差、等比数列的通项公式即可;
(2)直接使用错位相减法求之即可.
(2)直接使用错位相减法求之即可.
解答:
解:(1)因为a2,a5是函数f(x)=x2-7x+10的两个零点,则
,解得:
或
.
又等差数列{an}递增,则
,所以an=n,n∈N*…3分
因为点(bn,Sn)在直线y=-x+1上,则Sn=-bn+1.
当n=1时,b1=S1=-b1+1,即b1=
.
当n≥2时,bn=Sn-Sn-1=(-bn+1)-(-bn-1+1),即bn=
bn-1.
所以数列{bn}为首项为
,公比为
的等比数列,即bn=(
)n,n∈N*.…6分
(2)由(1)知:an=n,n∈N*且bn=(
)n,n∈N*,
则cn=an•bn=n•(
)n,n∈N*
所以Tn=1•
+2•(
)2+3•(
)3+…+n•(
)n①
Tn= 1•(
)2+2•(
)3+…+(n-1)•(
)n+n•(
)n+1②.
①-②得:
Tn=
+(
)2+(
)3+…+(
)n-n•(
)n+1=1-(n+2)(
)n+1.
所以Tn=2-(n+2)(
)n,n∈N*.…12分
|
|
|
又等差数列{an}递增,则
|
因为点(bn,Sn)在直线y=-x+1上,则Sn=-bn+1.
当n=1时,b1=S1=-b1+1,即b1=
| 1 |
| 2 |
当n≥2时,bn=Sn-Sn-1=(-bn+1)-(-bn-1+1),即bn=
| 1 |
| 2 |
所以数列{bn}为首项为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知:an=n,n∈N*且bn=(
| 1 |
| 2 |
则cn=an•bn=n•(
| 1 |
| 2 |
所以Tn=1•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以Tn=2-(n+2)(
| 1 |
| 2 |
点评:本题考查知识点等差、等比数列的通项公式;错位相减法求数列的和,考查分析问题解决问题的能力,

练习册系列答案
相关题目
已知a∈R,i是虚数单位,复数z=a+i,若z2为纯虚数,则z=( )
| A、1+i |
| B、-1+i |
| C、1+i或-1+i |
| D、2i或-2i |
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )
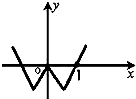

| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |