题目内容
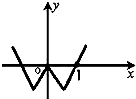
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )

| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |
考点:函数的图象
专题:函数的性质及应用
分析:由题意可得函数f(x)在(0,1)上单调递减,0<A<
-B,由此根据正弦函数的单调性可得0<sinA<sin(
-B)=cosB<1,从而得到f(sinA)>f(cosB).
| π |
| 2 |
| π |
| 2 |
解答:
解:由函数f(x)的导函数图象可得,在(0,1)上,f′(x)<0,函数f(x)在(0,1)上单调递减.
∵△ABC是以角C为钝角的钝角三角形,∴A+B<
,即 0<A<
-B,∴0<sinA<sin(
-B)=cosB<1,
∴f(sinA)>f(cosB),
故选:A.
∵△ABC是以角C为钝角的钝角三角形,∴A+B<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴f(sinA)>f(cosB),
故选:A.
点评:本题主要考查利用导数的符号研究函数的单调性,正弦函数在(0,
)上的单调性,属于基础题.
| π |
| 2 |

练习册系列答案
相关题目
已知过点A(a,4)和B(-2,a)的直线与直线2x+y-1=0垂直,则a的值为( )
| A、0 | B、-8 | C、2 | D、10 |
记a=log2
,b=70.3.c=(
)9.1,则a、b、c的大小关系是( )
| 5 |
| 6 |
| 1 |
| 7 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<a<c |
已知i为虚数单位,则复数
( )
| 1+2i |
| 2-i |
| A、1 | B、i | C、-1 | D、-i |
函数f(x)=
的定义域区间为( )
log
|
A、[1,
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(1,
|
如图是正方体ABCD-A′B′C′D′中,异面直线A′D与CD′所成的角是( )
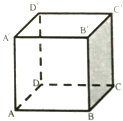

| A、30° | B、45° |
| C、60° | D、90° |